Calculate the volume of the Sphere, surface area of the Sphere and know the formulas.


Sphere Calculator



Result:

Radius: 0
Volume: 0
Surface Area: 0


What is a Sphere?

A sphere is a round solid in three-dimensional space. Like a circle in a two-dimensional space, a sphere is mathematically defined as the set of points which are the same distance ‘r’ from a specific point in three-dimensional space.



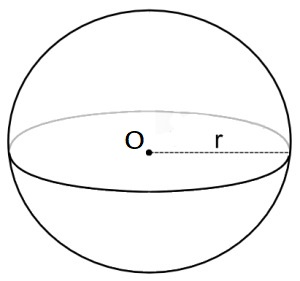
Sphere image - www.numeberbau.com


The distance ‘r’ is called the radius of the sphere. It is the distance from a given point which is the centre of the sphere. The longest straight line in the sphere passes through the centre and connects two points on the boundary of the sphere. This line is called the diameter and it is twice the radius. The figure below shows a sphere of radius r and centre O.

A sphere has only a curved surface, there are no edges, vertices or faces. It is a perfectly symmetrical body.

In three-dimensional geometry, the equation of a sphere is $$ (x-a)^2 + (y-b)^2 + (z-c)^2 = r^2 $$

where (a, b, c) indicates the coordinates of the centre of the sphere in the x, y and z axes respectively, and r is the radius.

Properties of Sphere

Given below are some properties of a sphere.

Volume – This is the total space occupied by the sphere in three-dimensional space.

Surface area – Surface area is the total area covered by the surface of the sphere.

Diameter – This is the longest line in the sphere. It passes through the centre and connects two points on the boundary of the sphere. The diameter is twice the length of the radius.

Sphere formulas

Given below are the formulas to calculate different properties of a sphere.

Volume $$ {4\over3}πr^3 \;cubic \,units $$
Surface area $$ {4\over3}πr^2 \; square \;units \;$$
Diameter $$ 2r \;units \;$$

Characteristics of a Sphere

Given below are the main characteristics of a sphere.

  • A sphere is mathematically defined as the set of points which are the same distance ‘r’ (known as the radius) from a specific point in three-dimensional space.
  • Like a circle, each point on the boundary of a sphere is at equal distance from the centre.
  • A sphere is a perfectly round, symmetrical body.
  • It has no vertices, edges or faces.
  • It does not have any flat surfaces.
  • A sphere is not a polyhedron because it has a curved surface. For the same reason, cylinders and cones are also not polyhedrons.
  • The diameter is the longest line in the sphere. It passes through the centre and connects two points on the boundary of the sphere.
  • The diameter of a sphere divides it into two equal hemispheres.

    • Areas of application

    Spheres occur frequently in everyday life. Some examples are as follows:

  • Balls used in sports are usually spherical in shape. Golf balls, despite being covered with dimples, are approximately spherical. Basketballs, footballs and tennis balls are also spheres, even though they may be covered by grooves, fibres or bumps.
  • Celestial bodies like the moon, planets and stars are nearly spherical in shape. Even the Earth is approximately a sphere, as it is slightly flattened at the poles.
  • Pool table balls need to be rounder than the balls used in most other games and sports. They are perfectly spherical, and do not have any bumps or undulations.
  • Ball bearings used in machinery and motors are spheres. Any roughness would lead to wearing out, and affect the performance of the machine.
  • Gyroscopes are perfectly spherical in shape.
  • Stable atomic nuclei are also spheres.
  • Glass pebbles and marbles are some other examples of spheres.

    • We now consider some examples making use of the sphere formulas.

    Question: A sphere has radius 4 cm. Find the volume, surface area, and length of the diameter.

    Answer: Here, the radius r = 4 cm

    The diameter = 2r = 8 cm.

    Volume of the sphere = 4/3 πr3 cm3 = 4/3 π(4)3 cm3 = 268.08 cm3

    Surface area = 4/3 πr2 cm2 = 4/3 π(4)2 cm2 = 67.02 cm2


    Question: The volume of a spherical ball is 5000 cm3. What is the radius of the ball?

    Answer: The volume of a sphere is V = 4/3 πr3 cm3

    So, the radius can be computed from the volume using the following formula

    $$ r \;= \; \sqrt[3]{3V\over4π} \;= \; \sqrt[3]{3(5000)\over4π} \;= \; \sqrt[3]{1193.662} \;≈ \; 10.61 \;cm $$

    Hence, the radius of the spherical ball is nearly 10.61 cm.

    See also:

    Share: