Trigonometry Calculator

Consider the right-angled triangle below.

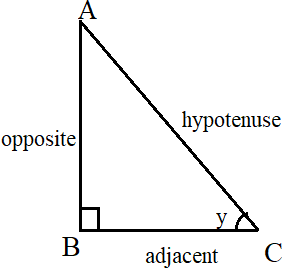
In this triangle, the right angle is at B. We wish to find the various trigonometric ratios of y. The side opposite the angle y is AB, the hypotenuse is AC and the adjacent side is BC. Therefore,

$$sin\, y\, =\, {opposite \over hypotenuse} \,=\,{AB\over AC} = a$$

$$cos\, y\, =\, {adjacent \over hypotenuse} \,=\,{BC\over AC} = b$$

$$tan\, y\, =\, {opposite \over adjacent} \,=\,{AB\over BC} = c$$

The tan function can also be written as

$$tan y = {sin y \over cos y}$$

The reciprocal functions are as follows.

$$cosec\, y\, =\, {1\over sin y} = {hypotenuse \over opposite} \,=\,{AC\over AB} = d$$

$$sec\, y\, =\, {1\over cos y} = {hypotenuse \over adjacent} \,=\,{AC\over BC} = e$$

$$cot\, y\, =\, {1\over tan y} = {adjacent \over opposite} \,=\,{BC\over AB} = f$$

The variables a, b, c, d, e, f indicates the respective trigonometric values of the angle y.

Inverse trigonometric functions are used to obtain the value of the angle when the sin, cos, tan, cosec, sec or cot values of the angle are known. They are defined as follows.

$$y = sin^{-1}({AB \over AC}) = sin^{-1} \,a $$

$$y = cos^{-1}({BC \over AC}) = cos^{-1} \,b $$

$$y = tan^{-1}({AB \over BC}) = tan^{-1} \,c $$

$$y = cosec^{-1}({AC\over AB}) = cosec^{-1} \,d $$

$$y = sec^{-1}({AC \over BC}) = sec^{-1} \,e $$

$$y = cot^{-1}({BC \over AB}) = cot^{-1} \,f $$

Given below are some properties of the trigonometric functions.

Angle – Denoted by a variable x or θ, this is the parameter for which the trigonometric value is calculated. On the other hand, the angle is the parameter which is calculated when the inverse trigonometric value inverse of the angle is known.

Domain – The values of the angle x for which we can compute sin(x), cos(x), tan(x), cosec(x), sec(x) and cot(x). For the inverse functions, the domain is the parameter for whose sine, cosine, tan, cosec, sec or cot is x.

Range – The values between which sin(x), cos(x), tan(x), cosec(x), sec(x) and cot(x) of any angle x lies. For the inverse trigonometric functions, the range consists of all the angles for which we can find arcsine(x), arccosine(x), arctan(x), arccosec(x), arcsec(x) and arccot(x).

Period - Horizontal length of one complete cycle of the trigonometric functions. The period for each of these functions have been illustrated in the graphs below.

Given below are the graphs of the trigonometric functions. In each of these graphs, the x axis denotes the angle in radians, and the y-axis denotes sin(x), cos(x), tan(x), cosec(x), sec(x) and cot(x) of that angle.

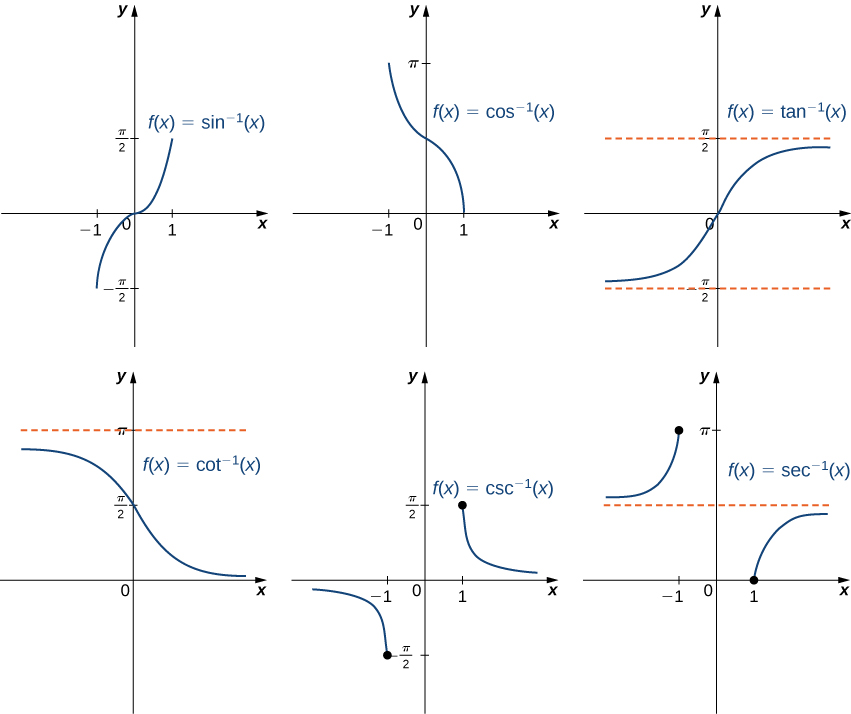
Given below are the graphs of the six inverse trigonometric functions. In each of the graphs below, the y-axis denotes the angle in radians, and the x-axis denotes arcsine(x), arccosine(x), arctan(x), arccosec(x), arcsec(x) and arccot(x) of that angle.

Given below are some commonly used values of the trigonometric functions.

Trigonometric functions and their inverses are used in mathematics and all branches of science, such as geometry, solid mechanics, navigation, and celestial mechanics to name a few.

Several real-life problems can be modelled using the trigonometric functions and their inverses. Some of these applications are:

• Sound waves and electromagnetic waves can be described using the sine and cosine functions.
• Trigonometric functions are used to calculate the angle of elevation which can help us determine the height of buildings or structures. It can also be used to calculate the angle of depression from the top of a building.
• In construction, trigonometric functions are used to measure fields and areas of land, for proper roof inclination, for building structures with specific angles, for making structures parallel and perpendicular and so on. Architects rely on trigonometry to calculate the slopes of roof, sun shades, and structural load.
• In physics, the trigonometric functions are used to model wave mechanics and oscillations. They are also used in the study of vectors.
• The direction of the wind plays an important role in the motion of an aircraft. Using vectors and trigonometric functions, the direction and speed of the wind can be calculated, and its effect on the aircraft motion.
• Mathematical concepts like Fourier series rely heavily on the knowledge of trigonometric functions.

---

---