Calculate the volume of the Rectangluar Prism, surface area of the Rectangluar Prism and know the formulas.
Rectangluar Prism Calculator
Result:
| Length(L): | 0 |
| Width (W): | 0 |
| Height (H): | 0 |
| Volume: | 0 |
| Surface Area: | 0 |
What is a Rectangluar Prism?
A rectangular prism is a three-dimensional figure with six sides, eight vertices and twelve edges. It has two parallel bases. It is also called a cuboid. Each of the six sides are rectangular in shape. It is called a rectangular prism because of its cross-section along the length.
The figure below shows a rectangular prism.

The length, height and width of the rectangular prism are indicated by l, h and w respectively. Both the bases and sides of the prism are rectangles. If the bases and sides of the prism were squares, then the resulting figure would be a cube.
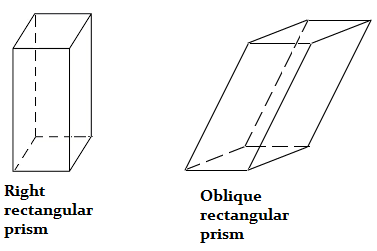
If each of the adjacent sides of a rectangular prism meet in a right-angle, it is called a right rectangular prism.
Properties of Rectangluar Prism
Given below are some properties pertaining to a rectangular prism.
Base – The surface at the two ends of the prism. For a rectangular prism, the base is always a rectangle.
Lateral surface – The sides of the rectangular prism connecting the two rectangles at the base, but excluding the base. The lateral surface is also composed of rectangles.
Face – The faces of the rectangular prism include the four rectangles on the lateral face, as well as the two rectangles at the base.
Volume – Volume indicates the total space occupied by the rectangular prism. It is equal to the product of the height of the prism and the area of the base.
Lateral surface area – The lateral surface area is the sum of the surface area covered by the faces, without the rectangles at the base.
Surface area – This is the total area covered by the prism. It is the sum of the lateral surface area and twice the area of the base of the rectangular prism.
Rectangluar Prism formulas
Below are the main formulas of a rectangular prism.
| Volume | $$ lbh \;cubic \,units $$ |
| Surface area | $$ 2(lb+bh+lh) \; square \;units \;$$ |
| Lateral surface area | $$ 2(l+w)h \;square \;units \;$$ |
Characteristics of a Rectangluar Prism
Given below are the main characteristics of a rectangular prism.
The figure below shows the two kinds of rectangular prisms.
Areas of application
Prisms like the rectangular and triangular prism are frequently seen in all walks of like. A rectangular prism is quite similar to a cube, except its sections are rectangular and the adjacent sides are unequal. It resembles a three-dimensional rectangle. Some common examples are cereal boxes, juice boxes, tissue boxes, notebooks and binders, boxes for wrapping presents, shirt boxes and aquariums to name a few. Large structures like storage sheds, barns, cargo containers, and buildings like houses and skyscrapers also take the shape of rectangular prisms.
We now consider some examples making use of the formulas of rectangular prisms.
Question: An aquarium is 90 m long, 60 m wide and 40 m wide. How much water can it contain?
Answer: To find the capacity of a rectangular prism, we need to find its volume.
In this problem, length l = 90 m, width w = 60 m and height h = 40 m.
Hence, the volume = l×w×h = 90×60×40 = 216000 m3
So, the aquarium can contain 216000 m3 of water.
Question: Anna is selling cookies in her neighbourhood. She needs to pack each order in a box to ship them. The dimensions of one cookie box is 2.3 in × 7 in × 4.6 in. The dimensions of the shipping box is 12 in × 12 in × 5.5 in. How many cookie boxes would fit into one shipping box?
Answer: For this problem, we need to compute the volume of each cookie box and the shipping box separately to find how many cookie boxes would fit into one shipping box.
Dimensions of the cookie box = 2.3 in × 7 in × 4.6 in
Volume of the cookie box = l×w×h = 2.3×7×4.6 = 74.06 in3
Dimensions of the shipping box = 12 in × 12 in × 5.5 in
Volume of the cookie box = l×w×h = 12×12×5.5 = 792 in3
To determine the number of cookie boxes in one shipping box, we divide the volume of the shipping box with that of the cookie box.
Number of boxes = 792/74.06 = 10.69
Therefore, each shipping box can contain a maximum of 10 cookie boxes.

