Calculate the volume of the Triangular Prism, surface area of the Triangular Prism and know the formulas.
Triangular Prism Calculator
Result:
| Side 1: | 0 |
| Side 2: | 0 |
| Side 3: | 0 |
| Height: | 0 |
| Volume: | 0 |
| Surface Area: | 0 |
What is a Triangular Prism?
A triangular prism is a polyhedron (or three-dimensional shape) having five faces, six vertices and nine edges. It consists of two triangular bases, and three rectangular sides. The edges of the prism join the corresponding sides.
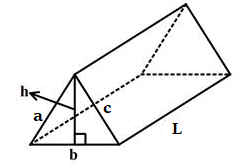
The figure above shows a triangular prism. The length of the prism is indicated by L, h is the height of the triangles at the bases, and a, b, c indicate the lengths of the sides of the triangle. If the triangles at the base are equilateral, and the sides are square, the prism is said to be uniform. A right triangular prism has rectangular sides. Otherwise, it is said to be oblique. In an oblique prism, the sides and the bases are not congruent to each other.
Properties of Triangular Prism
Given below are some properties of a triangular prism.
Base – The surface at the two ends of the prism. For a triangular prism, the base is always a triangle.
Lateral surface – The sides of the triangular prism connecting the two triangles at the base, but excluding the bases. The lateral face may be a rectangle or a square.
Face – The faces of the triangular prism include the three rectangles, as well as the two triangles at the base.
Volume – Volume indicates the space occupied by the triangular prism. It is equal to the product of the length of the prism and the area of the triangular base.
Lateral surface area – The lateral surface area is the area covered by the lateral surfaces.
Surface area – This is the total area covered by the prism. It is the sum of the lateral surface area and twice the area of the base of the triangular prism.
Triangular Prism formulas
Below are the main formulas of a triangular prism.
| Volume | $$ {1\over2}bhL \;cubic \,units $$ |
| Lateral surface area | $$ (a+b+c)L \;square \;units \;$$ |
| Surface area | $$ 2\sqrt{s(s-a)(s-b)(s-c)} \;+ \; (a+b+c)L \; square \;units \;$$ |
If a, b, and c indicate the sides of the triangle at the, the area of triangle is $$ 2\sqrt{s(s-a)(s-b)(s-c)} \; square \; units$$
where s is the semi-perimeter, $$ s \;= \; {{a+b+c}\over2} $$
If the height of the triangular base is known, then the area of the triangular base is 1/2 bh square units
In that case, the total surface area is $$bh+(a+b+c)L square units$$
Characteristics of a Triangular Prism
Given below are the main characteristics of a Triangular prism.
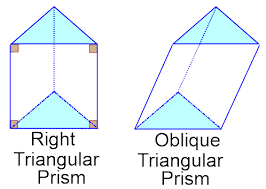
The figure below shows the two kinds of triangular prisms.
Areas of application
Triangular prisms can be seen occurring naturally in mineral crystals. The regular geometry of this three-dimensional body finds several applications for designing buildings and simple products of everyday use. Chocolate wrappers, like Toblerone for instance, are sometimes in the shape of a triangular prism. Some other common examples are camping tents and triangular roofs of buildings. Many barns and sheds also have roofs built in this shape.
We now consider an example making use of the formulas for a triangular prism.
Question: Find the volume and surface area of the following triangular prism.
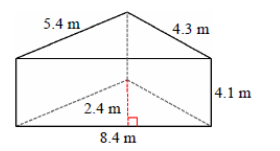
Answer: In the given figure, the lengths of the sides of the triangle at the base are 5.4 m, 4.3m and 8.4m.
Hence, a = 5.4 m, b = 8.4 m and c = 4.3 m.
The height of the triangle at the base has been marked as h = 2.4m.
Also, the length of the prism is L = 4.1 m.
The lateral surface area $$ = \;(a+b+c)L \;m^2 \\ = \; (5.4+8.4+4.3)4.1 \;= \;74.21 \,m^2 \\ $$
The total surface area $$ = \;bh+(a+b+c)L \;m^2 \\ = \;8.4 \,× \,2.4 \,+ \,74.21 \;m^2 \\ = \;20.16\,+\,74.21 \;m^2 \;= \;94.37 \;m^2$$
The volume is calculated using the formula $$ = \; {1\over2} \;bhL \;m^3 \\ = \;1/2 \; × \, 8.4 \,× \, 2.4 \,× \,4.1 \; m^3 \\= \;41.328 \;m^3 $$

