Arcsine Calculator
Result:
| Angle in degrees: | 0 |
| Angle in radian: | 0 |
What is arcsine?
Arcsine is essentially the inverse of the sine function. In a right-angled triangle, the sine of an angle y is defined as the ratio of the side opposite to the angle, to the hypotenuse. When we take arcsine of this ratio, we get the measure of the angle y.
Consider the right-angled triangle below.
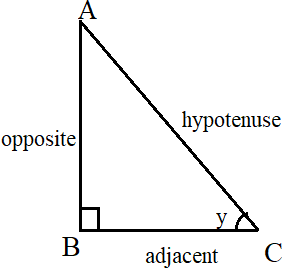
In this triangle, the right angle is at B. Sine of the angle y is given by
$$sin\, y\, =\, {opposite \over hypotenuse} \,=\,{AB\over AC} = x$$
To find the angle y when the ratio AB/AC is known, we use the following formula for arcsine
$$y\, =\, sin^{-1}{opposite \over hypotenuse} \,=\,sin^{-1} x$$
The expression y = sin-1x, means that sin y = x , when -π/2 ≤ y ≤ π/2 and -1 ≤ x ≤ +1.
Arcsine(x)=y is defined as the set of all angles whose sine is x. It should be noted here that the -1 is not an exponent and hence, sin-1x ≠ 1/sinx .
Properties of the arcsine function
Given below are some properties of the arcsine function.
Angle – The angle is the parameter which is calculated when sin inverse (or arcsine) of the angle is known.
Domain – The arcsine of the parameter whose sine is x. This value goes from -1 ≤ x ≤ 1.
Range – The angles for which we can find sin^(-1)x. This value is -π/2≤ y ≤π/2 radians or -90 ≤ y ≤ +90 degrees.
Given below is a graph of the arcsine function.

In the above graph, the y-axis denotes the angle in radians, and the x-axis denotes arcsine of that angle. The red curve denotes the arcsine function. For any value of x between -1 and +1, the arcsine function returns a value between -π/2 and π/2 radians (or -90⁰ to 90⁰). For example, when x=1, y=arcsine(x) returns y= π/2 radians. This means that sin(π/2) = 1.
If the arcsine graph is compared to the sine graph, one would see that the arcsine graph can be obtained from the sine graph by simply interchanging the horizontal and vertical axes.
Values of arcsine(x)
Given below are some commonly used values of arcsine(x).
| y=sin-1x in degrees | y=sin-1x in radians | x |
|---|---|---|
| -90 | $$-π\over2$$ | -1 |
| -60 | $$-π\over3$$ | $$-√3\over2$$ |
| -45 | $$π\over4$$ | $$-1\over√2$$ |
| -30 | $$π\over6$$ | $$-1\over2$$ |
| 0 | 0 | 0 |
| 30 | $$π\over6$$ | $$1\over2$$ |
| 45 | $$π\over4$$ | $$1\over√2$$ |
| 60 | $$π\over3$$ | $$√3\over2$$ |
| 90 | $$π\over2$$ | 1 |
The value of arcsine(x) can be positive or negative, depending on the value of x. For example, arcsine(-1/2) is negative, whereas arcsine(1/2) is positive. This is because sin-1(-x)=-sin-1x.
This has been illustrated below.
In this figure, the x-axis denotes the arcsine values, whereas the y-axis denotes the angle θ. Arcsine(x) will be positive when 0≤ θ ≤ π/2 (in Quadrant 1), and negative when -π/2 ≤ θ < 0 (in Quadrant 4).

We can also note that
sin(sin-1(x))=x when -1 ≤ x ≤ +1.
For example, sin(sin-1(1/2)) = sin 30⁰ = 1/2.
Similarly, sin-1(sin x) = x when -π/2 ≤ x ≤ +π/2.
For example, sin-1(sin π/4) = sin-1(1/√2) = π/4.
If we need to find the arcsine of the sine of an angle which does not lie between -π/2 and π/2, the correct angle can be found by either adding or subtracting 2π radians until we get an angle in the range of -π/2 to +π/2, which is the range of the arcsine function. This is because 2π is the period of the sin function.
Arcsine formula
From a right-angled triangle, the arcsine formula can be computed as
$$y = sin^{-1}{AB \over AC} = sin^{-1} \,x$$
where AB is the opposite side and AC is the hypotenuse, and y is the angle which can be calculated.
Like sin(x), there is no well-known Taylor series approximation for the arcsine function. However, a series expansion can be obtained using binomial expansion or integration.
The formula thus obtained, where -1 < x < 1, is given below.
$$ sin^{-1}x = x + {1\over2}\,{x^3\over2} + {1.3\over2^2\,2!}{x^5\over5} + {1.3.5\over2^3 3!}{x^7\over7} + {1.3.5.7\over2^4 4!}{x^9\over9} + ...$$
OR
$$ sin^{-1}x = \int_0^x {1\over\sqrt{1-t^2}} =x + {1\over2}\,{x^3\over2} + {1.3\over2^2\,2}{x^5\over5} + {1.3.5\over2^3 3!}{x^7\over7} + {1.3.5.7\over2^4 4!}{x^9\over9} + ...$$
Areas of application
Trigonometric functions as well as the inverse trigonometric functions are used widely in engineering, geometry and physics. They are also used to solve trigonometric equations describing real-life problems.
In this section, we consider some example problems involving the use of the arcsine formula.
Question: Compute sin-1(sin 9π/5).
Answer:The angle 9π/5 radians does not lie between -π/2 and +π/2, but it can be reduced to a smaller angle by removing all the full rotations of 2π radians until we get an angle in the range of -π/2 to +π/2, which is the range of the arcsine function.
Hence, 9π/5 radians can be written as 9π/5 - 2π = -π/5 radians.
Therefore, sin-1(sin 9π/5) = sin-1 (sin(-π/5) ) = -π/5
Question: In the given triangle, find the angle y when the measures of the three sides are given in centimetres.

Answer: In the given right-angled triangle, the sides are as follows. We need to find the angle y.
Using the sine formula, we obtain
$$ sin\, y = {opposite\over hypotenuse} = {8\over10} = 0.8$$
$$ sin\, y = 0.8$$
$$ y = sin^{-1}(0.8) ≈ 53.13⁰$$
Hence, the angle y measures 53.13⁰ (approximately).

