Sector calculator
Sector Calculator
Result:
| Circumference of Sector: | 0 |
| Area of Sector: | 0 |
| Arc length of Sector: | 0 |
What is a Sector?
In two-dimensional geometry, a sector is the region of a circle bounded by two radii of the circle, and the arc in between. The arc is a small part of the circumference, and the radii are the endpoints of this arc. It is like a ‘pizza slice’ of the circle. Given below is a figure of a sector.
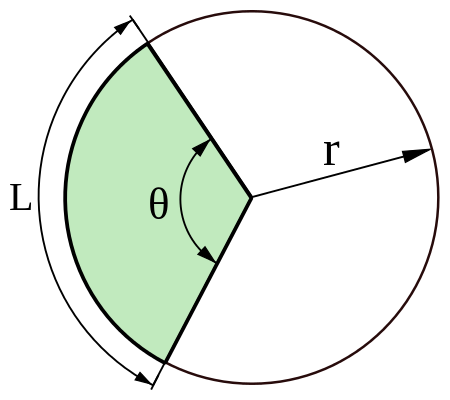
In the above figure, θ denotes the angle made by the sector at the centre of the circle, r is the radius and L is the arc length. A sector divides the circle into two portions – a major sector and a minor sector.
The minor sector is the smaller sector of the circle, whereas the major sector is the larger one. The minor sector of a circle subtends a smaller angle at the centre than the major sector. The major sector is the also the region having a greater area. In the figure above, the minor sector has been shaded in green, whereas the major sector is in white.
A sector which has the central angle as 180⁰ divides the circle into two equal parts. Such a sector is bound by the diameter of the circle and a semicircle.
Depending on the central angle, sectors are often given special names, such as quadrants (when the angle is 90⁰), sextants (60⁰) or octants (45⁰). A quadrant is one-fourth of a circle, a sextant is one-sixth and an octant is one-eighth.
Properties of a Sector
The figure below highlights the different parts of the Sector.
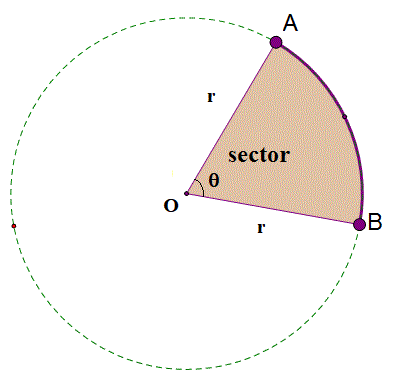
Given below are the definitions of the parts of the Sector.
Centre – The middle point of the circle.
Radius – The line segment which connects the centre of the circle to any point on the boundary of the circle. Here, OA and OB are the radii of the circle which measure r units in length.
Angle of the sector – The angle subtended at the centre of the circle by the two radii which constitute the sector. In the figure above, the angle of the sector is marked θ.
Major sector – The region of the circle having greater area. In the figure above, the major sector is white.
Minor sector – The region of the circle having a smaller area. The minor sector has been shaded in the figure above.
Arc – It is a part on the curve of a circle.
Arc Length – The distance covered by the curved portion of the circle which makes up the arc of the sector. In this figure, the portion AB on the circumference of the circle constitutes the arc length of the given sector.
Quadrant – The sector which is formed when the angle made by it is 90⁰.
Area – Region occupied by the sector.
Perimeter – Total distance covered by the boundary of the sector. It is the sum of the arc length and the two radii.
Sector formulas
Below are the formulas to calculate different properties of a sector. Here, r denotes the radius of the circle and θ is the angle of the sector.
| Area | $$ r^2 ({θ\over2}) \;square \;units (if \;θ \;is \;in \;radians) \\ πr^2 ({θ⁰\over360⁰}) \;square \;units ( \,if \;θ \;is \;in \;degrees)$$ |
| Arc Length | $$ 2πr ({θ\over360}) \;units $$ |
| Perimeter | $$ 2r \;+ \; ({2πr \;θ\over360}) \;units $$ |
Characteristics of a Sector
Given below are the main characteristics of a sector.
- A sector is a part of a circle bounded by two radii of the circle, and the arc in between.
- Depending on the angle made by the sector at its centre, a sector may be given different names.
- A sector which has the central angle as 180⁰ divides the circle into two equal parts.
- The major sector is the part of the circle having greater area, whereas the minor sector is the region with the smaller area.
- The perimeter of the sector is the sum of the arc length and the two radii.
Areas of application
Like circles, sectors also have various real-life applications. The most common one would be the slices obtained when we cut up a pizza. Major and minor sectors also indicate the fractions of a circle. Sectors are frequently used in pie charts for visualizing statistical data. Sectors are also used to design and construct freeway exits, when a ‘clover leaf’ style of interchange is used.
We now consider an example where the sector formulas are applied.
Question: Find the area and perimeter of a sector whose radius is 10 cm, and the angle is 60⁰.
Answer: The radius r = 10 cm, and angle θ = 60⁰.
Area: $$ πr^2 \; ({θ⁰\over360⁰}) \;= \; π×10×10× (60/360) ≈ 52.36 \;cm^2 $$.
Perimeter: $$ = 2r+(2πr ({θ\over360})) \\ = 2×10+(2π×10× 60/360) = 20+10.472 = 30.472 \;cm $$
Hence, area covered by the sector is 52.36 cm2 and the perimeter is 30.472 cm.

