ArcLength Calculator
Result:
| Arc length of Sector: | 0 |
| Circumference of Sector: | 0 |
| Area of Sector: | 0 |
What is Arc Length?
An arc is a part on the curve of a circle. The arc length is essentially the distance covered by the curved portion of the circle which makes up the arc. This has been illustrated in the figure below.

The above figure depicts a circle of radius r and centre O. AB is an arc of the circle. In other words, AB is a small part on the curve of the circle. The angle made by this arc at the centre is θ. The region of the circle, bounded by the two radii (OA and OB) and the arc AB, is called the sector.
The arc length is the distance between the two endpoints of the arc, which lie on the boundary of the circle. The red line between A and B denotes the length of the arc determined using the radius and the angle at the centre.
Properties of Arc Length
The figure below highlights the different parts of an arc.
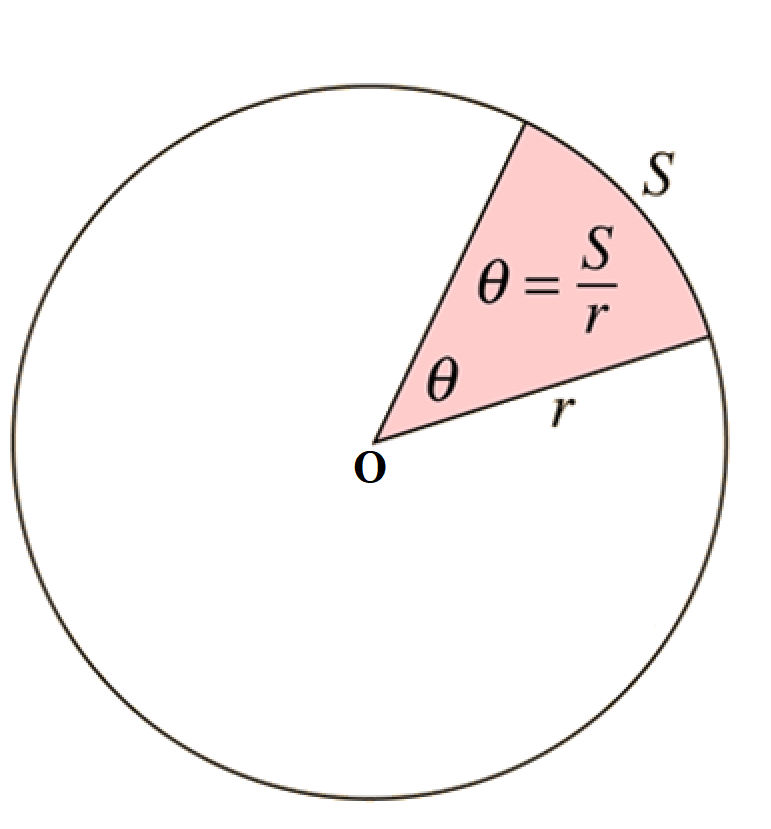
Given below are the definitions of the parts of an arc.
Centre – The middle point of the circle.
Radius – The line segment which connects the centre of the circle to any point on the boundary of the circle.
Angle of the arc – The angle subtended at the centre of the circle by the two radii which constitute the sector. In the figure above, the angle is marked θ.
Sector – It is a region of the circle bounded by two radii of the circle, and the arc in between. In the figure, the sector has been shaded.
Arc Length – The distance covered by the curved portion of the circle which makes up the arc of the sector. In this figure, the portion S on the circumference of the circle constitutes the arc length.
Area – Region occupied by the sector.
Perimieter – Total distance covered by the boundary of the sector. It is the sum of the arc length and the two radii.
Arc Length formulas
Below are the formulas to calculate arc length. Here, r denotes the radius of the arc length and θ is the angle at the centre.
| Arc length S | $$ θr \;units \;(when \;θ \;is \;in \;radians)$$ |
| Arc length S | $$ 2πr ({θ⁰\over360⁰}) \;units \;(when \;θ \;is \;in \;degrees)$$ |
| Arc length in integral form | $$ \int_a^b \sqrt{1+({dy\over dx})^2} \;units$$ |
Areas of application
Arc lengths are used in conjunction with sectors for several real-life applications. The arc length formula is used to find the perimeter of the sector. Major and minor sectors also indicate the fractions of a circle. The arc length of the minor sector is smaller than that of the major sector.
Sectors are used in pie charts for visualizing statistical data. The distance covered by a Ferris wheel when it moves halfway through and stops can be described using an arc length.
We now consider some examples where the arc length formula is used.
Question: Calculate the arc length if the radius of the arc is 8 cm and the angle at the centre is 45⁰.
Answer: For the given problem, radius r = 8 cm and θ = 45⁰.
Then the arc length is $$ 2πr ({θ⁰\over360⁰}) = 2π x 8 ({45⁰\over360⁰}) = 16π ({1\over8}) = 6.28 cm $$
Hence, the length of the arc is 6.28 cm.
Now we consider a real-life problem.
Question: You are riding a Ferris wheel. You start at the bottom of the ride and make it half way around before the ride stops to load more passengers. If the radius of the wheel is 30 feet, what is the length of the arc you have traveled?
Answer: Radius r of the Ferris wheel = 30 feet.
When the Ferris wheel travels half way around, it makes an angle of θ = π radians at the centre.
So, the length of the arc travelled = r θ = 30π ≈ 94.25 feet.
Therefore, when the Ferris wheel travels half way round and then stops to load more passengers, the length of the arc travelled is 94.25 feet.

