Pyramid calculator
Pyramid Calculators
Result:
| Surface Area: | 0 |
| Volume: | 0 |
Result:
| Surface Area: | 0 |
| Volume: | 0 |
What is a Pyramid?
A pyramid is a figure in three-dimensional geometry having a polygon at its base, and every corner of the base meets at a point known as the apex (or vertex) of the pyramid. The edges of the base form a triangle with the vertex. The number of such triangles formed depends on the number of sides in the base. In this section, we will focus on pyramids having square and rectangle as their bases.
The figure below shows these two kinds of pyramids.
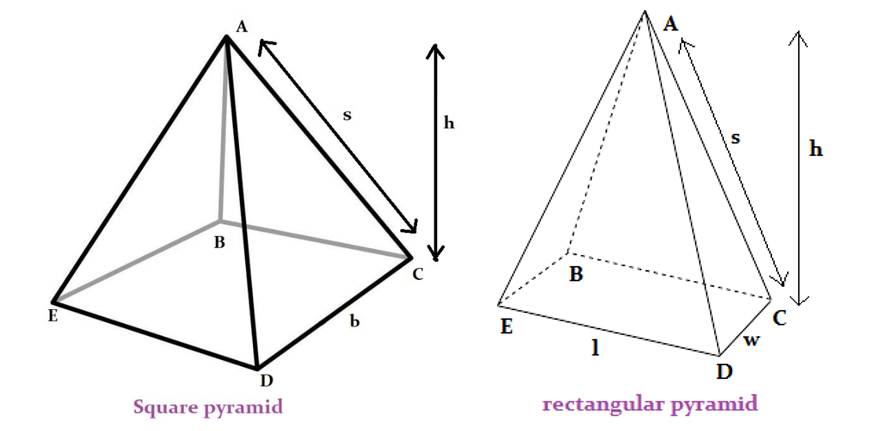
In both these figures, the vertex is A. In the square pyramid, the base is a square of side ‘b’. In the rectangular pyramid, the base is a rectangle of length ‘l’ and width ‘w’. The height of the pyramid is the distance between the base and the vertex, denoted by ‘h’. The slant height of the pyramid is the distance between the vertex and one edge of the base along a line segment in the triangle connecting these two. In the figures above, the slant height from the vertex A to one of the sides CD has been marked as ‘s’.
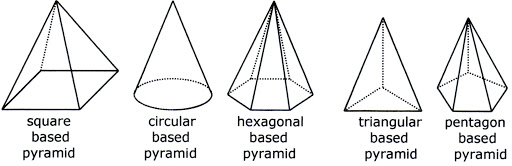
Apart from the square and rectangular pyramids, there may be other types of pyramids named after the polygon at the base. This polygon may be a square, rectangle, triangle, pentagon, hexagon, circle and more. This has been illustrated below. The pyramid having a circular base is essentially a cone.
Properties of Pyramid
Given below are some properties of a pyramid.
Volume – This is the total space occupied by the pyramid.
Lateral surface area – The lateral surface area of a pyramid is the area excluding the surface area of the base. It is the area of the slanted portion of the pyramid.
Surface area – Surface area is the total area covered by the pyramid. It is equal to the sum of the lateral surface area and the area covered by the polygon at the base.
Pyramid formulas
Given below are the formulas of a pyramid.
The general formula for the volume and surface area of a pyramid is as follows:
Surface area = base area + 1/2 (number of sides in the base × slant height×length of the base)
Volume = 1/3 x base area × height
For a square pyramid:
Here, b indicates the length of the base, h is the height of the pyramid, and s is the slant height.
| Volume | $$ {1\over3}b^2h \;cubic \,units $$ |
| Area of the base | $$ b^2 \;square \;units \;$$ |
| Lateral surface area | $$ 2bs \;square \;units \;$$ |
| Surface area | $$ 2bs \,+ \,b^2 \; square \;units \;$$ |
For a rectangluar pyramid:
Here, l indicates the length of the base, w is the width, h is the height of the pyramid, and s is the slant height.
| Volume | $$ {1\over3}lwh \;cubic \,units $$ |
| Area of the base | $$ lw \;square \;units \;$$ |
| Lateral surface area | $$ {1\over2}(2l+2w)s \;square \;units \;$$ |
| Surface area | $$ {1\over2}(2l+2w)s \,+ \,lw \; square \;units \;$$ |
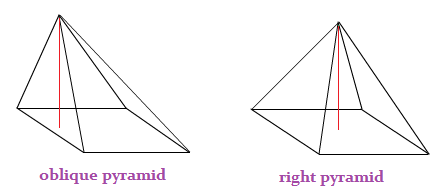
Characteristics of a Pyramid
Given below are the main characteristics of a pyramid.
These two kinds of pyramids have been shown below.
Areas of application
Pyramids are not very common in everyday life. However, in Egyptian culture, they are symbolically significant, so many designers and artists incorporate the pyramidal shape in their artwork, sculpture or architecture. The most notable example of pyramids are the pyramids of Giza in Egypt, the Great American Pyramid in Memphis, USA and the glass Louvre pyramid in Paris, France. Some other commonly observed pyramids are cheese graters and the slanted roofs of houses.
We now consider an example making use of the pyramid formulas.
Question: Find the volume and surface area of a rectangular pyramid when the height is 7.5 cm, the slant height is 9 cm, length of the base is 10 cm and the width is 5 cm.
Answer: According to this question, the height h = 7.5 cm, slant height s = 9 cm, length l =10 cm and width w = 5 cm.
We can directly use these values in the pyramid formulas.
Volume = $$ {1\over3} \;lwh \;cubic \;units \;= \;{1\over3} \; (10)(5)(7.5) \;= \; 125 \;cm^3 $$
Area of the base = $$ lw \;square \;units \;= \;(10)(5) \;= \;50 cm^2 $$
Lateral surface area = $$ {1\over2} \, (2l+2w)s \;square \;units \;= \;{1\over2} \,(2×10+2×5)9 \;= \; {1\over2}×30×9 \;= \;135 \;cm^2$$
Total surface area = $$ {1\over2}(2l+2w)s \,+ \,lw \; square \;units \;= \;135+50 \;= \;185 \;cm^2$$

