Ellipse calculator
Ellipse Calculator
Result:
| Circumference of Ellipse: | 0 |
| Area of Ellipse: | 0 |
What is an Ellipse?
In two-dimensional geometry, an ellipse is the set of all points in a plane such that the sum of their distances from two fixed points in the plane is a constant. These two fixed points are known as the foci of the ellipse. Given below is a figure of an ellipse.
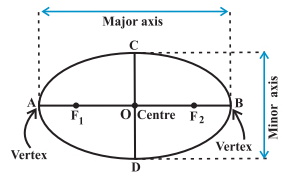
In the above figure, the two foci are F1 and F2. A line segment is drawn through the foci. The midpoint of this line segment is the centre of the ellipse. Here, O indicates the centre.
The ellipse is defined by its axes. The major axis of the ellipse is the longest diameter of the ellipse, passing through the centre and connecting two points on the boundary. This is the broad part of the ellipse. The minor axis is the smallest diameter of the ellipse, passing through the centre. It is the narrow part of the ellipse. In the figure above, AB is the major axis and CD is the minor axis.
The equation of an ellipse, when (h, k) denotes the coordinates of the centre, is as follows.
$$ {({x-h})^2\over a^2} \;+ \;{({y-k})^2\over b^2} \; = \; 1 $$
Here, a and b denote the lengths of the semi-major and semi-minor axes respectively.
In the above figure, the length of the semi-major axis = OB = ‘a’, and the length of the semi-minor axis = OA =’b’, and a > b.
If the centre of the ellipse is the origin (0, 0), the equation may be written as
$$ {x^2\over a^2} \;+ \;{y^2\over b^2} \; = \; 1 $$
A circle is a special case of the ellipse when the major axis and minor axis are equal in length. In that case, the equation is written as
$$ {x^2\over a^2} \;+ \;{y^2\over a^2} \; = \; 1 $$
or
$$ {x^2 \;+ \;y^2} \; = \; a^2 $$
Here, ‘a’ simply indicates the radius of the circle.
Properties of an Ellipse
The figure below highlights the different parts of the ellipse.
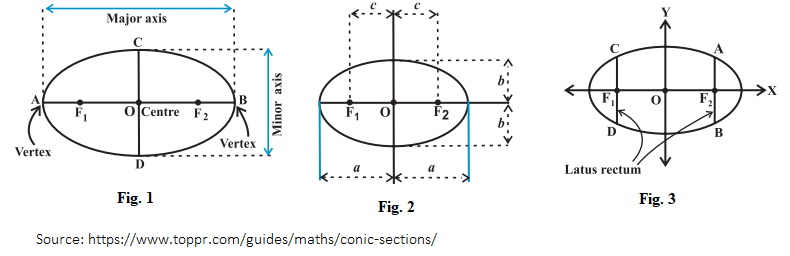
Given below are the definitions of the parts of an ellipse.
Foci – The ellipse is the locus of all the points, the sum of whose distance from two fixed points is a constant. These two fixed points are the foci, labelled F1 and F2.
Major axis – The line joining the two foci. This is the longest diameter of the ellipse, marked by AB.
Minor axis – The line which is perpendicular to the major axis. This is the smallest diameter of the ellipse, marked by CD.
Semi-major axis – Half the length of the major axis, indicated by ‘a’.
Semi-minor axis – Half the length of the minor axis, indicated by ‘b’.
Focal length – Distance between one of the foci and the centre of the ellipse, indicated by ‘c’. When c=0, the ellipse becomes a circle.
Vertex – The endpoints of the major axis. Here, it is A and B.
Centre – The midpoint of the line segment joining the two foci.
Eccentricity – Ratio of the distance from the centre of the ellipse to one of the foci and one of the vertices. The eccentricity measures how ‘un-round’ the ellipse is.
Latus rectum – A line perpendicular to the major axis, and passing through one of the foci, and the endpoints of the line lie on the ellipse. These have been marked in Fig. 3
Area – Region occupied by the ellipse.
Perimeter – Total distance covered by the boundary of the ellipse.
Ellipse formulas
Below are the formulas to calculate different properties of an ellipse. Here, ‘a’ denotes the semi-major axis and ‘b’ is the semi-minor axis.
| Perimeter | $$ 2π \, \sqrt{{a^2+b^2}\over 2} \; units $$ |
| Area | $$ πab \; square \; units $$ |
| Eccentricity ‘e’ | $$ {c\over a} \; units \;\; or \;\; \sqrt{1-{b^2 \over a^2}} \; units $$ |
| Focal Length ‘c’ | $$ \sqrt{{a^2-b^2}} \;units $$ |
| Length of the latus rectum | $$ {2b^2 \over a} \;units $$ |
Characteristics of an Ellipse
Given below are the main characteristics of an ellipse.
- The ellipse is a conic section which is created when a plane cuts a cone at an angle with the base.
- A circle is a special case of the ellipse, where the semi-major and semi-minor axes measure the same and is called the radius. In a circle, the two foci are at the same point called the centre of the circle.
- An ellipse has two focal points.
- The eccentricity of an ellipse lies between 0 and 1.
- The shape of an ellipse resembles a flattened circle.
Areas of application
Many real-world situations can be represented using ellipses. If an ellipse is rotated about the major axis, one would obtain a rugby ball. The paths of heavenly bodies such as comets, planets, satellites and moons can be described using ellipses. Some buildings are constructed with elliptical domes so that a person whispering at one focus can be heard by someone else standing at the other focus. One such building is the whispering gallery in the US Capitol building.
We now consider an example where the ellipse formulas are used.
Question: Find the lengths of the semi-major and semi-minor axes, foci, vertices, eccentricity and area of the ellipse.
$$ {x^2 \over 9} \; + \; {y^2 \over 4} \; = \; 1 $$
Answer: The denominator of x2 is larger than that of y2. So, the major axis is along the x-axis.
Comparing the above equation with the equation of an ellipse, we get a2 = 9 and b2 = 4. Hence, a=3 units and b=2 units. These are the lengths of the semi-major and semi-minor axes respectively.
Now,
| Focal length: | $$ c \; = \; \sqrt{a^2-b^2} \; = \; \sqrt{9-4} \; = \sqrt{5} \; units $$ |
| Eccentricity: | $$ e \; = \; {c\over a} \; = \; {\sqrt{5}\over 3} \; = 0.75 \; units $$ |
| Foci are: | $$ {(\pm c, 0)} \; = \; (\sqrt{5},0) \; and \; (-\sqrt{5},0) $$ |
| Vertices are: | $$ {(\pm a, 0)} \; = \; (3,0) \; and \; (-3,0) $$ |
| Area: | $$ πab \; = \; 6π \; ≈ \;18.85 \;square \;units $$ |

