Circle calculator - Calculate the Area, Diameter, Circumference of a Circle.
Circle Calculator
Result:
| Circumference of Circle: | 0 |
| Area of Circle: | 0 |
| Diameter of Circle: | 0 |
What is a Circle?
In two-dimensional geometry, a circle is a closed curve in which all the points on its boundary are at a fixed distance from a given point, which is designated the centre of the circle. Given below is a figure of a circle.
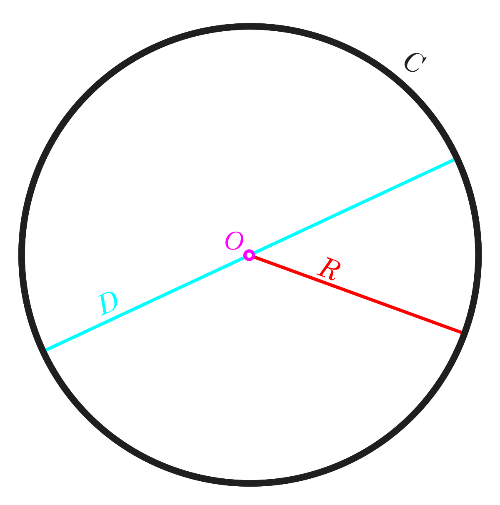
In the above figure, O indicates the centre of the circle. The distance between the centre and all the points on the circumference (or the boundary) of the circle is called the radius, marked with R. The circumference is marked C. The diameter D is a line segment connecting two points on the boundary of the circle, and passing through the centre O. The diameter is twice the length of the radius.
The equation of a circle is (x-a)2+(y-b)2 = r2, where (a, b) denotes the coordinates of the centre of the circle, and r is the length of the radius.
If the centre of the circle is the origin (0, 0), the equation may be written as x2 + y2 = r2.
Properties of Circle
The figure below highlights the different parts of the Circle.

Given below are the definitions of the parts of the Circle.
Centre – The middle point of the circle.
Radius – The line segment which connects the centre of the circle to any point on the boundary of the circle.
Diameter – The line segment drawn between two points on the circle, which goes through the centre. It is the longest possible distance from one end of the boundary of the circle to the other end. The diameter of a circle is twice the radius.
Chord – The line segment with its endpoints on the boundary of the circle. The diameter is the only chord which passes through the centre of the circle. It is the largest chord of the circle.
Tangent – A line which touches the circle at a single point. At the point of contact, the tangent is perpendicular to the radius.
Secant – A line which cuts the circle at two points. It is also known as the extended chord. The chord is the part of the secant which lies within the circle.
Arc – It is a part on the curve of a circle.
Sector – It is a region of the circle bounded by two radii of the circle, and the arc in between. It is like a ‘pizza slice’ of the circle.
Segment – It is a region of the circle between an arc and the endpoints of a chord. Segments of a circle do not contain the centre.
Area – Region occupied by the circle.
Circumference – Total distance covered by the boundary of the circle.
Circle formulas
Below are the formulas to calculate different properties of a circle. Here, r denotes the radius of the circle.
| Perimeter | $$ 2πr \;units $$ |
| Area | $$ πr^2 \;square \;units \;$$ |
| Diameter | $$ 2r \;units$$ |
Characteristics of a circle
Given below are the main characteristics of a circle.
- A circle is a closed curve in a plane which is formed by a set of points equidistant from the centre. This distance is called the radius of the circle.
- The diameter is twice the radius. It is also the largest chord of the circle.
- The diameter divides the circle in two equal parts called semicircles.
- Two or more circles having the same radius are said to be congruent to each other.
- The tangent line is always perpendicular to the radius of the circle at the point of contact.
Areas of application
Some commonly observed circles in real life are pizzas, tyres, Ferris wheels, rings, steering wheels of vehicles, and buttons, to name a few. Circles are present in various forms in everyday life, in both natural and man-made creations. Many household items like plates, cups and bowls have circles in their design.
We now consider an example where the circle formulas are applied in real life.
Question: Find the diameter, area and circumference of a circular lawn which has a radius of 7 metres. What would be the cost of putting a fence around the lawn for 0.75$ per metre?
Answer: The lawn under consideration is a circle having radius r = 7 metres.
Diameter of the lawn = 2×7 = 14 metres.
Area of the lawn= πr2 = π(7)2 ≈ 153.94 square metres
Circumference of the lawn = 2πr = 2π × 7 = 43.98 ≈ 44 metres
To find the cost of putting a fence around the lawn, we need to multiply the circumference (that is, the boundary of the circle) with the cost per metre.
Hence, total cost for putting a fence around the lawn = 44 × 0.75$ = 33$

