Law of Cosines to find the sides and angle.
Law of Cosines Calculator
Result:
| Side a: | 0 |
| Side b: | 0 |
| Side c: | 0 |
| Angle ∠A: | 0 |
| Angle ∠B: | 0 |
| Angle ∠C: | 0 |
What is the Law of Cosines?
The Law of Cosines (or Cosine rule) denotes the relationship between the lengths of the sides of a triangle and the cosine of one of the angles. It states that, if the lengths of two sides of the triangle and the angle between them is known, then we can compute the length of the third side. Consider the triangle below.
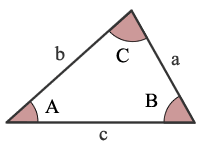
In the triangle shown above;
a, b and c are the lengths of the sides of the triangle, and the angles opposite to them are A, B and C respectively.
Then, the Law of Cosines states that
$$ a^2 = c^2 + b^2 - 2bc \, cos A $$
$$ b^2 = a^2 + c^2 - 2ac \, cos B $$
$$ c^2 = a^2 + b^2 - 2ab \, cos C $$
The Law of Cosines is a generalization of the Pythagoras theorem, which holds only for right-angled triangles. If the angle C is 90⁰, then cos C=0. Then the Law of Cosines reduces to $$c^2=a^2 + b^2 $$
Properties of a triangle
Given below are some properties of a triangle.
Perimeter – Total distance covered by the boundary of the triangle.
Area – Region covered by the triangle.
Triangle formulas
Below are the formulas pertaining to a triangle
Perimeter: $$ a+b+c$$
Area (using Heron’s formula): $$ \sqrt{s(s-a)(s-b)(s-c)}$$ where s is the semi-perimeter, s=(a+b+c)/2
Law of cosines formulas
The Law of Sines is as follows:
$$ a^2 = c^2 + b^2 - 2bc \, cos A $$
$$ b^2 = a^2 + c^2 - 2ac \, cos B $$
$$ c^2 = a^2 + b^2 - 2ab \, cos C $$
Below are the formulas to calculate the different Angles:
To find A: $$ a^2 = c^2 + b^2 - 2bc \, cos A $$ Hence, $$ A = cos^{-1}({{b^2+c^2-a^2}\over 2bc}) $$
To find B: $$ b^2 = a^2 + c^2 - 2ac \, cos B $$ Hence, $$ B = cos^{-1}({{a^2+c^2-b^2}\over 2ac}) $$
To find C: $$ c^2 = a^2 + b^2 - 2ab \, cos C $$ Hence, $$ C = cos^{-1}({{b^2+a^2-c^2}\over 2ab}) $$
Below are the formulas to calculate the different Sides:
To find side a: $$ a = \sqrt{b^2+c^2-2bc\,cos A} $$
To find side b: $$ b = \sqrt{a^2+c^2-2ac\,cos B} $$
To find side c: $$ c = \sqrt{a^2+b^2-2ab\,cos C} $$
Areas of application
This law can be used to find the unknown lengths or angles of a triangle. To find an unknown value, three values must be known. The Cosine rule helps to find the length of a side, when two of the sides and the angle between them is known, and for finding the angles of a triangle when the lengths of the three sides are known.
Let us assume that we want to find the angle A. For this, we need to know the lengths of the sides a, b and c. To find angles B and C also, only the knowledge of the side lengths is sufficient. This calculation follows the side-side-side (SSS) theorem.
If we want to find the length of any side, say ‘b’, we need to know the opposite angle B and the lengths of the other two sides, a and c. By using alternate forms of the Law of Cosines, we can compute the all the unknown sides and angles. This calculation follows the side-angle-side (SAS) theorem.
In this section, we consider some example making use of the cosine law.
Question: In the triangle below, the lengths of the sides have been given as a=10cm, b=15cm, c=20cm. Find the three angles.
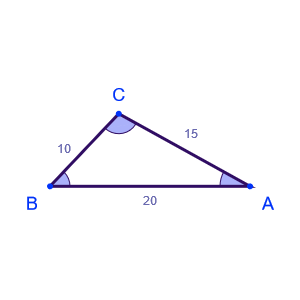
Answer: In the given triangle, the side opposite angle A is ‘a’. Here, a=10cm. It is also given that b=15cm and c=20cm.
We begin by finding A.
$$ A = cos^{-1}({{b^2+c^2-a^2}\over 2bc}) = cos^{-1}({{15^2+20^2-10^2}\over 2 * 15 * 20}) $$ $$ A = cos^{-1}({525 \over 600}) = cos^{-1}({7\over8}) ≈ 28.955⁰ $$Now we find B and C.
$$ B = cos^{-1}({{a^2+c^2-b^2}\over 2ac}) = cos^{-1}({{10^2+20^2-15^2}\over 2*10*20 }) $$ $$ B = cos^{-1}({275 \over 400}) = cos^{-1}({11\over16}) ≈ 46.568⁰ $$ $$ C = cos^{-1}({{b^2+a^2-c^2}\over 2ab}) = cos^{-1}({{15^2+10^2-20^2}\over 2*15*10 }) $$ $$ C = cos^{-1}({-75 \over 300}) = cos^{-1}({-1\over4}) ≈ 104.478⁰ $$Hence, the three angles are A≈28.955⁰, B≈46.568⁰ and C≈104.478⁰
Question: In the triangle below, the lengths of the sides b and c are 60cm and 40cm respectively, and A=34⁰. Find the length of the side a.
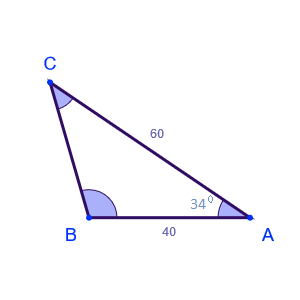
Answer: In the given triangle, b=60cm, c=40cm and A=34⁰.
To find the length of the side a, we can make use of the Law of Cosines.
$$ a = \sqrt{b^2+c^2-2bc\,cos A} $$ $$ a = \sqrt{60^2+40^2-2*60*40\,cos 34} $$ $$ a = \sqrt{1220.62} ≈ 34.937 cm $$Therefore, the length of side a is approximately 35cm.

