Volume calculator for 3D Shapes.
Volume Calculators
Result:
| Volume of Cone: | 0 |
Result:
| Volume of Cylinder: | 0 |
Result:
| Volume of Cube: | 0 |
Result:
| Volume of Sphere: | 0 |
Result:
| Volume of Rectangluar Prism: | 0 |
Result:
| Volume of Triangular Prism: | 0 |
What is Volume?
Volume is the quantity which measures the space enclosed by a three-dimensional body. It defines the space that a substance or shape contains. Finding the volume of a body helps us determine the amount of a substance required to fill the body, for example, the amount of water that would fill a water bottle or bathtub.
Volume Formulas
Below are the formulas to calculate the volumes of three-dimensional shapes.
Cone
In three-dimensional geometry, a cone is a shape which becomes narrower smoothly from a flat base (sometimes, circular) to a point called the apex or vertex. A cone is formed from line segments, lines or half-lines connecting a common point, the vertex, to all the points on the base. Given below is the figure of a cone.
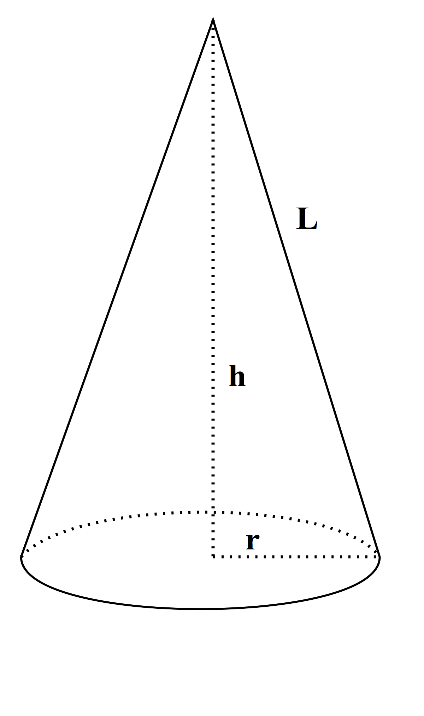
In this figure, the base of the cone is a circle of radius r. The distance from the centre of the base to the vertex of the cone is called the height h of the cone. The distance from the vertex to any point on the circumference of the base is called the slant height of the cone indicated by L.
The volume of a cone can be found using the formula $$ {1\over3}πr^2\,h \;cubic \;units $$
Cylinder
A cylinder is a three-dimensional shape which consists of two parallel circular bases separated by a distance. The circular cases are joined by a curved surface at a fixed distance from their centres. The centres of the two circular bases are connected by a line which is called the axis of the cylinder. The figure below shows a cylinder.

In this figure, the two circular bases have the same radius r. They are separated by a distance h. This is known as the height of the cylinder.
The volume of the cylinder is calculated as $$ πr^2 \, h \;cubic \;units $$
Cube
A cube is a three-dimensional solid body with six square sides (or faces), twelve edges and eight vertices. Three of the sides meet at each vertex. It is also called a regular hexahedron. The cube is a special case of a cuboid (or rectangular prism) where the length, breadth and height are equal. The figure below shows a cube of side ‘d’ units.

The volume of a cube is $$ d^3 \;cubic \;units $$
Rectangular prism
A rectangular prism is a three-dimensional figure with six sides, eight vertices and twelve edges. It has two parallel bases. It is also called a cuboid. Each of the six sides are rectangular in shape. The figure below shows a rectangular prism.

The formula for the volume of a rectangular prism is $$ lbh \;cubic \;units, $$ where l, b and h denote the length, breadth and height of the rectangular prism as shown in the figure.
Sphere
A sphere is a round solid in three-dimensional space. Like a circle in a two-dimensional space, a sphere is mathematically defined as the set of points which are the same distance ‘r’ from a specific point in three-dimensional space. This distance ‘r’ is called the radius of the sphere, and the given point is called its centre. The figure below shows a sphere of radius r and centre O.
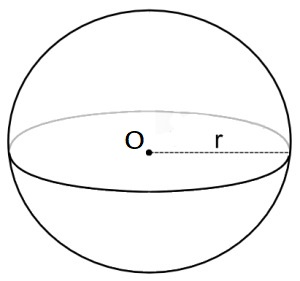
The formula for the volume of a sphere is $$ {4\over3}πr^3 \;cubic \;units $$
Triangular prism
A triangular prism is a polyhedron (or three-dimensional shape) having five sides, six vertices and nine edges. It consists of two triangular bases, and three rectangular sides. The edges of the prism join the corresponding sides.
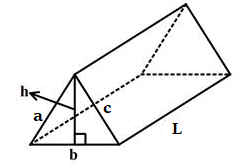
The figure above shows a triangular prism where the length of the rectangular side is L, b is the length of the triangular base and h is the height of the base.
The volume of the prism is the product of the area of the triangular base and the length of the rectangular side.
Hence, the volume is $$ {1\over2} \,lbh \;square \;units. $$
Areas of application
Volume measures how much space a fluid occupies. When we’re measuring ingredients for a recipe, filling up our water bottles, buying fuel for the car or adding detergent to the washing machine, volume formulas frequently come up in daily life. Volume is necessary whether we are measuring liquids or drinking amounts.
- When buying fuel for a vehicle, the volume of petrol or diesel the tank holds determines the purchase amount. The quantity of fuel bought is a volume calculation.
- In the kitchen, measuring cups, spoons and flasks indicate the volume of ingredients used for a particular recipe.
- Water flow from sprinklers, taps and hoses in the house determine water usage, and eventually, the water bill for the residents. The water used is also measured in volumes.
- In swimming pools, a certain volume of cleaners and chemicals are added to the water, depending on the capacity of the pool.
- For cleaning houses or washing clothes, a specific amount of the cleaning product is used, which is measured in volume.

