Mixed Fraction numbers - Addition, Subtraction, Multiplication and Division
Mixed Fraction Calculator
Input Number 1
Input Number 2
Fraction number operations:
| Operation | Result |
| Number 1: | 0 |
| Number 2: | 0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
0 |
What is a mixed Fraction?
A fraction is a number of the form a/b, where b ≠ 0. It represents some part of a whole. Fractions are of three types: Proper fraction, improper fraction and mixed fraction.
In a proper fraction, the numerator is lesser than the denominator, whereas it is the opposite for an improper fraction. A mixed fraction (also called a mixed number) is a fraction which has a whole part and a fractional part. For example, 2 ¼ is a mixed fraction, where 2 is the whole number and ¼ is the fractional part.
For performing any calculations, the mixed fractions need to be converted to improper fractions first. For example, 2 ¼ in mixed fraction form is 9/4. Consider an example of a mixed fraction below.
Consider a pizza cut into 4 slices. Suppose one whole pizza and one half of another pizza have been given as shown here. The one whole pizza represents the whole number, which is 1 in this case, and ½ is the fractional part. Combining these two together gives the mixed fraction 1 ½, which indicates one whole pizza and ½ part of another pizza.
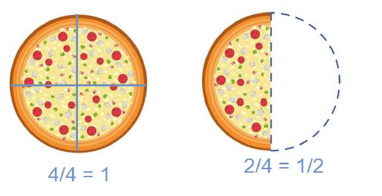
Now, if there were two whole pizzas present along with the half pizza, the whole number would be 2, and the fractional number would be ½. In mixed fraction form, this is 2 ½.
Mixed fractions, like all other types of fractions, obey all the usual properties of fractions such as commutative property under addition and multiplication, and the distributive property. The inverse of a mixed fraction is the reciprocal of the corresponding improper fraction, and the identity element is 0 (under addition) and 1 (under multiplication). In the fractional part of a mixed fraction, the fraction is always a proper fraction (the numerator is lesser than the denominator).
Converting a mixed fraction to an improper fraction
Consider the mixed fraction 1 2/5. We try to convert this mixed fraction into an improper fraction.
1) First, multiply the whole number by the denominator. This gives us 5.
2) Now we add up the 5 with the numerator, to get 7.
3) Hence, for the mixed fraction, the denominator stays the same as the mixed fraction, whereas the numerator becomes 7. The corresponding improper fraction is 7/5.
Mixed Fraction formulas
To perform arithmetic operations on mixed fractions, they need to be converted to improper fractions first. The formulas for different arithmetic operations on mixed fractions are as follows.
| Formula | Example |
|---|---|
| Addition: For addition, a least common denominator needs to be found so that all the fractions being added have the same denominator. $$ {a\over b} + {c\over d} = {{a*d}\over{b*d}}+{{c*b}\over{d*b}}={{ad+bc}\over bd} $$ | For example, $$ 1{2\over5} + 2{3\over4} = {7\over5}+{11\over4} = {{7*4}\over{5*4}} + {{11*5}\over{4*5}} = {{28+55}\over 20} = {83\over 20} = 4{3\over20} $$ |
| Subtraction: For subtraction also, a least common denominator needs to be found. $$ {a\over b} - {c\over d} = {{a*d}\over{b*d}}-{{c*b}\over{d*b}}={{ad-bc}\over bd} $$ | For example, $$ 1{2\over5} - 2{3\over4} = {7\over5} - {11\over4} = {{7*4}\over{5*4}} - {{11*5}\over{4*5}} = {{28-55}\over 20} = -{27\over 20} = -1{7\over20} $$ |
| Multiplication: Unlike addition or subtraction, for multiplying fractions, we do not need to find the least common denominator. $$ {a\over b} * {c\over d} = {{a*c}\over{b*d}} $$ | For example, $$ 1{2\over5} * 2{3\over4} = {7\over5} * {11\over4} = {77\over 20} = 3{17\over20} $$ |
| Division: When dividing one fraction by the other, the first fraction is multiplied by the reciprocal of the second one. $$ {{a\over b} \over {c\over d}} = {a\over b}*{d\over c} = {{a*d}\over {b*c}} $$ | For example, $$ {1{2\over5} \over 2{3\over4}} = {{7\over5} \over {11\over4}} = {{7*5}\over{4*11}} = {{7*4}\over{5*11}} = {28\over55} $$ |
Steps for arithmetic operations on mixed fractions
The steps for different arithmetic operations on mixed fractions are as follows
1) Addition and subtraction:
a) First convert the mixed fractions to improper fractions.
b) To add or subtract two or more mixed fractions, we first need to find the least common denominator of all the mixed fractions.
c) For each mixed fraction, multiply the denominator with the number so that the least common denominator is obtained. Multiply the numerator also with the same number.
d) Repeat this step for all the mixed fractions.
e) For addition, add the numbers in the numerator, and for subtraction, subtract them.
f) Reduce the mixed fraction to its lowest term.
2) Multiplication:
a) First convert the mixed fractions to improper fractions.
b) Unlike addition and subtraction, we do need to find the least common denominator for multiplication and division of mixed fractions. In this case, first multiply all the numerators together, and the denominators together.
c) Finally, reduce the fraction to its lowest term or as a mixed fraction.
3) Division:
a) First convert the mixed fractions to improper fractions.
b) For division, we first need to know which mixed fraction is being divided by the other.
c) Keep the first fraction as it is.
d) Replace the second fraction with its reciprocal.
e) Multiply the two fractions, and reduce the result to its lowest term or as a mixed fraction.
Areas of application
We encounter mixed fractions all around us. Consider a problem making use of mixed fractions.
Question: For baking bread, Amy used of 15 2/5 ounces of flour. She then added water, followed by ¼ ounce of yeast. Her dough weighed 24 ounces. She forgot to weigh the water she had added individually. How much water was added?
Answer: To find the amount of water used, we can set this up in the form of an equation. $$ 15{2\over5}+x \; =\; 24 $$
Here, 15 2/5 is the quantity of flour, the unknown ‘x’ is the quantity of water and 24 is the final weight of the dough. To find x, we first convert the mixed fraction into an improper fraction, and then use the usual rules of fraction subtraction. 15 2/5 as an improper fraction is 77/5.
$$ {77\over5}+x \; = \; 24 \\ x=24-{77\over5} $$
$$ x={{24*5}\over{1*5}} - {{77*1}\over{5*1}} $$
$$ x= {{120-77}\over5} = {43\over5} = 8{3\over5} $$
Therefore, the quantity of water used was 8 3/5 ounces.

