Fraction to Percentage - Convert the mixed fraction number into Percentage value
Fraction to Percentage
Mixed Fraction Number
Result Summary:
| Type | Result |
| Given Fraction number | 0 |
| Percentage value | 0 |
What are fractions and percentages?
A fraction is a number of the form a/b, where b ≠ 0. It represents some part of a whole. Fractions are of three types: Proper fraction, improper fraction and mixed fraction. In a proper fraction, the numerator is lesser than the denominator, whereas it is the opposite for an improper fraction. A mixed fraction (also called a mixed number) is a fraction which has a whole part and a fractional part. For example, 2 ¼ is a mixed fraction, where 2 is the whole number and ¼ is the fractional part. 3/5 is another example of a fraction. Since the numerator is lesser than the denominator, it is a proper fraction.
A percentage is a fraction with the denominator as 100. When we express some fraction as a percentage, we express how many parts of the 100, the fraction denotes. For example, the fraction ½ can be written as 50%, because ½ is equivalent to 50/100. For proper fractions, the corresponding percentage is a number less than 100. For improper and mixed fractions, the numerator of the percentage is greater than the denominator, and hence the percentage is greater than 100%. For example, the fraction 13/12 corresponds to 108.33%
Consider a pizza cut into 4 slices.
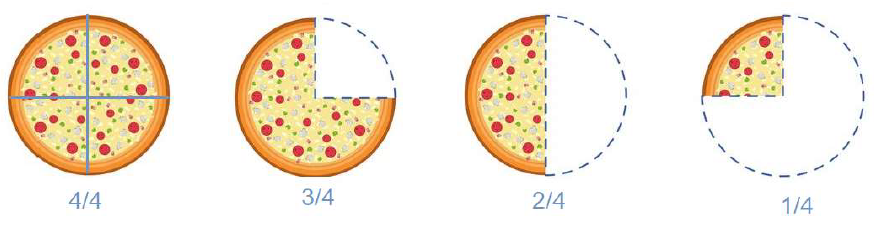
When all four slices of the pizza are present, the fraction is written as 4/4. The 4 in the denominator indicates that 4 slices make up the whole pizza. This corresponds to 100%. When one slice of the pizza has been eaten, 3 slices remain which is indicated by the fraction 3/4, which is equivalent to 75%. When 2 slices are eaten, 2 slices remain, indicated by 2/4 or 1/2, which is 50%. Finally, when only one slice remains, it is represented by 1/4 or 25%.
Fractions to percentage formula
If the fraction is denoted by a/b, where a is the numerator and b is the denominator, then the formula for converting this to a percentage is $$ {a\over b}*100 \; = \; p% $$
Here, p denotes the percentage.
Consider the problem of the pizza getting divided into 4 slices described above.
i) When 4 slices are present, the fraction is written as 4/4. $$ {4\over4}*100 = 100% $$
ii) 3 slices remaining is indicated by the fraction 3/4. $$ {3\over4}*100 = 0.75 * 100 = 75% $$
iii) When 2 slices remain, the fraction is 2/4 or 1/2. $$ {1\over2}*100 = 0.5 * 100 = 50% $$
iv) When 1 slice remains, the fraction is 1/4. $$ {1\over4}*100 = 0.25 * 100 = 25% $$
Converting a fraction to a percentage – proper fractions
The steps for converting a fraction to a percentage are described below. For this, we consider the fraction 5/8.
1) First, divide the numerator by the denominator of the fraction using long division. This would give the decimal value of the fraction. 5/8 expressed as a decimal is 0.625.
2) Now multiply the decimal number with 100 to convert it into a percentage.
In this case, 0.625 × 100 = 62.5.
Hence, 5/8 expressed as a percentage is 62.5%. This number is lesser than 100 because 5/8 is a proper fraction.
If the fraction is not in its simplest form, the same method can still be carried out.
For example, consider the fraction 6/8. The result of dividing 6 by 8 is 0.75, which is 75% as a fraction. If we had reduced this fraction in the initial step, the fraction would be 3/4. The decimal value of this fraction is also 0.75 which is equivalent to 75%.
Converting a fraction to a percentage – improper and mixed fractions
We now consider a mixed fraction 5(3/4). For mixed fractions, we first need to convert this to an improper fraction. 5(3/4) as an improper fraction is 23/4.
Now perform a long division on the numerator by the denominator to obtain the corresponding decimal value. 23/4 as a decimal is 5.75.
Finally, multiply this decimal number with 100. 5.75 multiplied by 100 gives 575. Therefore, $$ 5{3\over4} = {23\over4} = 57.5 = 575% $$
The percentage is greater than 100 because the numerator of the fraction was greater than the denominator.
Areas of application
Fraction to percentage conversion is frequently used in mathematical and scientific computations. Sometimes, it helps to express a fraction or decimal value of a quantity as a percentage to assess its influence on the overall system. This has been described using an example problem.
Question: Selina enrolled in a discrete mathematics course which was for a total of 200 credits for an entire semester. Out of these, the end-semester examination is worth 100 credits, the mid-semester examination is for 50 credits, homework assignments are worth 40 credits, and classroom participation is worth 10 credits. What is the percentage of each of these units in the entire course?
Answer: To find the percentage of credits for each of these units in the entire course, we can list them out as fractions first.
End-semester examination = 100 credits out of 200 = 100/200 or 1/2.
Mid-semester examination = 50 credits = 50/200 = 1/4.
Homework assignments = 40/200 = 1/5.
Classroom participation = 10/200 = 1/20.
We first convert each of these fractions to their corresponding value and then multiply by 100 to obtain the percentage. This has been tabulated below.
| Units | Fraction of the credits | Decimal value | Percentage |
|---|---|---|---|
| End-semester examination | 100/200 = 1/2 | 0.5 | 0.5 × 100 = 50% |
| Mid-semester examination | 50/200 = 1/4 | 0.25 | 0.25 × 100 = 25% |
| Homework assignments | 40/200 = 1/5 | 0.2 | 0.2 × 100 = 20% |
| Classroom participation | 10/200 = 1/20 | 0.05 | 0.05 × 100 = 5% |
Hence, the end-semester examination has the greatest influence on Selina’s discrete math grade, while classroom participation has the least.

