Cosine Calculator
Cosine Calculator
Result:
| cos(X): | 0 |
What is cos?
Cos (or cosine) is a trigonometric function. In a right-angled triangle, the cos of an angle x is defined as the ratio of the side adjacent to the angle, to its hypotenuse.
$$cos\, x = {adjacent \over hypotenuse}$$
Consider the right-angled triangle below.
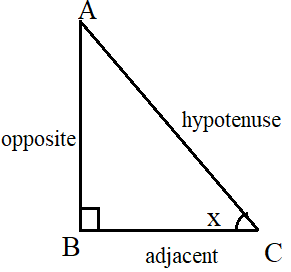
In this triangle, the right angle is at B. We wish to find the cos of x. The side adjacent to the angle x is BC, and the hypotenuse is AC. Therefore,
$$cos\, x\, =\, {adjacent \over hypotenuse} \,=\,{BC\over AC}$$
Properties of the cosine function
Given below are some properties of the cos function.
Angle – Denoted by a variable x or θ, this is the parameter for which the cos value is calculated.
Domain – The values of the angle x for which we can compute cos(x). This value goes from -infinitive to +infinitive.
Range – The values between which cos(x) of any angle x lies. This value is -1≤ cos(x) ≤1.
Period – Horizontal length of one complete cycle of the cos function. The period for cos(x) is 2π radians or 360⁰.
Given below is a graph of the cosine function.
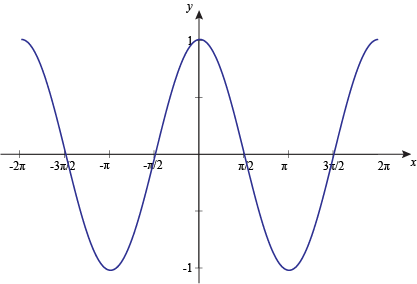
Like the sin function, the cos function is also periodic in nature, with a period of 2π radians (or 360⁰). This means that, the graph repeats itself every 2π radians. In the above graph, the x axis denotes the angle, and the y-axis denotes cos of that angle.
From the graph, it can be seen that cos(x) starts from +1 then it falls to -1. From there, it goes upwards again. It attains the value +1 at 2π radians and -1 at π radians.
The only difference between the sine and cos graph is that, the sine graph starts at 0 at 0⁰, whereas the cos graph has the value +1 at 0⁰.
Values of cos(x)
Given below are some commonly used values of cos(x).
| Angle x in degrees | Angle x in radians | cos(x) |
|---|---|---|
| 0 | 0 | 0 |
| 30 | $$π\over6$$ | $$√3\over2$$ |
| 45 | $$π\over4$$ | $$1\over√2$$ |
| 60 | $$π\over3$$ | $$1\over2$$ |
| 90 | $$π\over2$$ | 0 |
| 120 | $$2π\over3$$ | $$-1\over2$$ |
| 135 | $$3π\over4$$ | $$-1\over√2$$ |
| 150 | $$5π\over6$$ | $$-√3\over2$$ |
| 180 | π | -1 |
| 270 | $$3π\over2$$ | 0 |
| 360 | 2π | 1 |
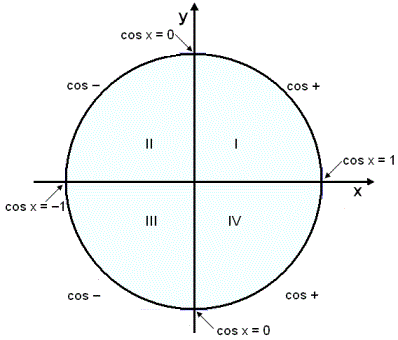
The value of cos(x) can be positive or negative, depending on where the angle x lies in the four quadrants. For example, cos 45⁰ is positive, whereas cos 135⁰ is negative. This has been illustrated below.
| Quadrant | x in degrees | x in radians | Sign of the cos function | Range of cos values |
|---|---|---|---|---|
| 1 | 0⁰ to 90⁰ | $$0\, to\, {π\over2}$$ | + | 0 < cos(x) < 1 |
| 2 | 90⁰ to 180⁰ | $${π\over2}\, to\, π$$ | - | -1 < cos(x) < 0 |
| 3 | 180⁰ to 270⁰ | $$π\, to\, {3π\over2}$$ | - | -1 < cos(x) < 0 |
| 4 | 270⁰ to 360⁰ | $${3π\over2}\, to\, 2π$$ | + | 0 < cos(x) < 1 |
If the angle x does not lie between 0⁰ to 360⁰ (or 0 to 2π radians), it can be expressed as a multiple, sum or difference of one of the above angles, and then its cos value can be determined.
Cos formula
To calculate cos(x) from a right-angled triangle, the formula used is
$$cos\, x = {adjacent \over hypotenuse}$$
A different formula is used when we wish to calculate the cos of an angle in a calculator. This can be done using the Taylor series approximation for the cos function, when the angle x is in radians. The formula is;
$$ cos\, x = 1 - {x^2\over2!} + {x^4\over4!} - {x^6\over6!} + {x^8\over8!} - ...$$
The more terms taken, the more accurate is the approximation.
Areas of application
Trigonometric functions like the sine and cosine function are used to describe simple harmonic motion because the oscillatory motion of an object represents the graphs of these two trigonometric functions. When an object is undergoing simple harmonic motion, the distance covered by the object is expressed using either sin or cos functions. The cos function, and formulas involving it, are also frequently used to solve trigonometric problems or prove trigonometric identities.
In this section, we consider some example problems involving the use of the cos function.
Question: A 25 feet ladder rests against a wall, making an angle of 45⁰ with the horizontal. How far from the wall is the base of the ladder?
Answer:This problem can be visualized as below.
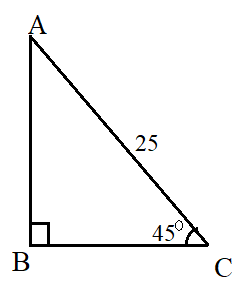
The ladder is denoted by AC, whose length is 25 feet. The wall is denoted by AB. We need to find the distance between the wall and the base of the ladder, which is BC.
Using the cos formula, we can compute how far the wall is from the base of the ladder.
Hence, BC ≈ 17.68 feet.
The ladder is almost 17.68 feet away from the wall.
In the next example, we use the Taylor series formula to find the cos of an angle.
Question: Find the value of cos 25⁰ ?
Answer: For using the Taylor series formula, the angle x must be converted to radians. To convert 25⁰ to radians, we multiply by π and divide by 180.
Angle x in radians = 25π/180 = 0.43633
$$ cos\, x = 1 - {x^2\over2!} + {x^4\over4!} - {x^6\over6!} + {x^8\over8!} - ...$$
$$ cos\, 0.43633 = 1 - {0.43633^2\over2!} + {0.43633^4\over4!} - {0.43633^6\over6!} + {0.43633^8\over8!} - ...$$
cos 0.43633 = 1 - 0.095192 + 0.001510 - 0 + 0 - …
cos 0.43633 = 0.906318
Hence, cos 25⁰≈0.9063
Now, consider the case of an angle which does not lie between 0⁰ and 360⁰.
Question: Find the value of cos 540⁰ ?
Answer: The angle 540⁰ does not lie between 0⁰ and 360⁰. We try to reduce the value of this angle by removing all the full rotations of 360⁰.
Now, 540⁰ = 360⁰ + 180⁰.
Removing one full rotation shows us that cos 540⁰ is equivalent to cos 180⁰.
From the cos graph, as well as the table of listed values, we can see that cos 180⁰ = -1.
Hence, cos 540⁰ = -1.

