Calculate the volume of the Cube, surface area of the Cube and know the formulas.
Cube Calculator
Result:
| Side: | 0 |
| Volume: | 0 |
| Surface Area: | 0 |
What is a Cube?
A cube is a three-dimensional solid body with six square sides (or faces), twelve edges and eight vertices. Three of the sides meet at each vertex. It is also called a regular hexahedron. The cube is a special case of a cuboid (or rectangular prism) where the length, breadth and height are equal.

The above figure shows a cube of side ‘d’ units.
Some alternate names of a cube are square parallelepiped and equilateral cuboid. All the faces of a cube are squares. Each face of the cube is connected by four vertices.
Properties of Cube
Given below are some properties of a cube.
Volume – The volume of a cube is the total space occupied by it.
Surface area – This is the total area covered by the cube in three-dimensional space.
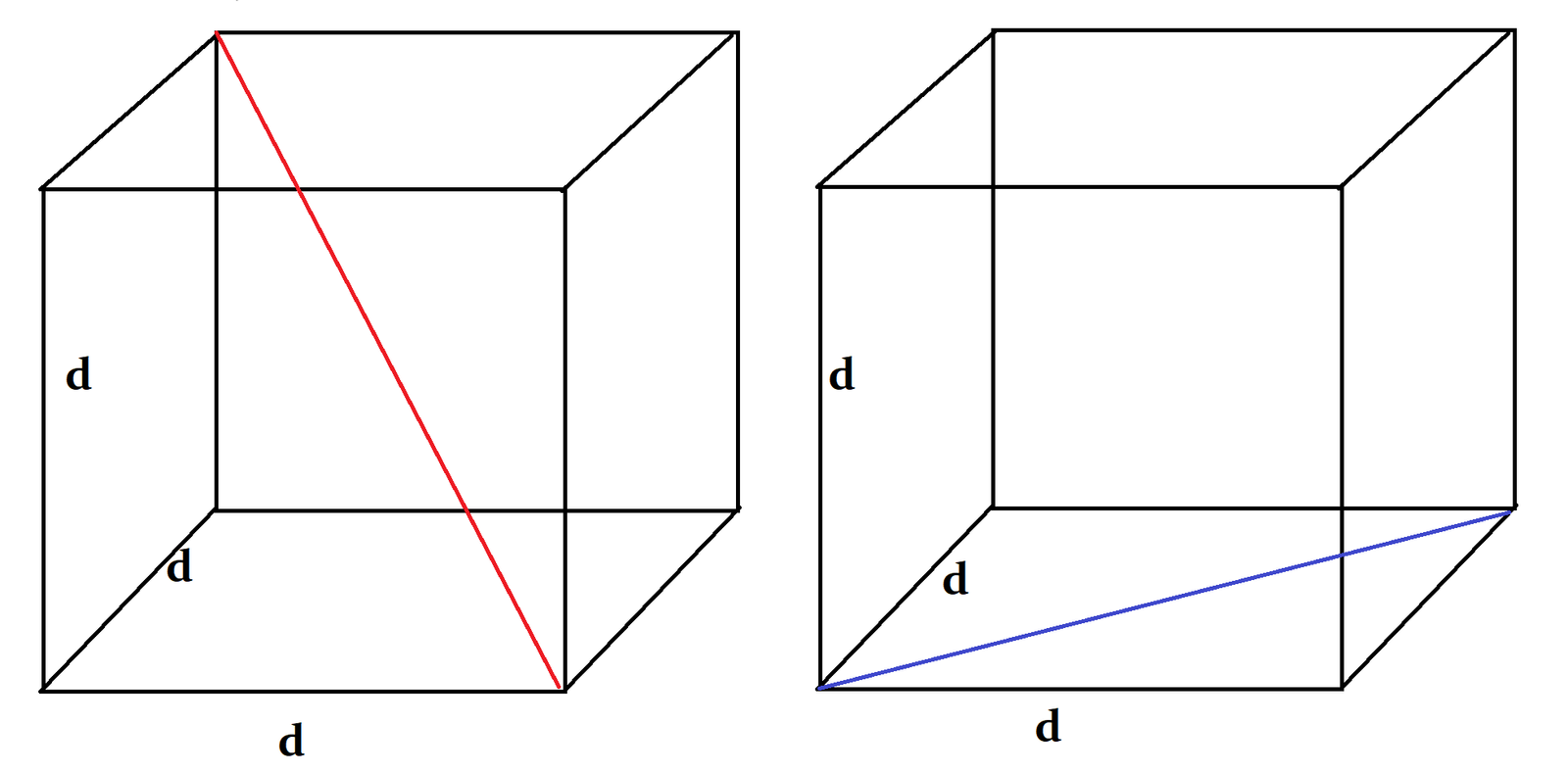
Diagonal of a cube – The diagonal of a cube is the main diagonal which passes through the centre of the cube. It is not the same as the diagonal of the face of a cube.
The figure below shows a cube of length ‘d’ units. The red line passing through centre of the cube is the main diagonal, whereas the blue line indicates the diagonal of the face of a cube.
Cube formulas
Given below are the formulas of a cube.
| Volume | $$ d^3 \;cubic \,units $$ |
| Surface area | $$ 6d^2 \;square \;units \;$$ |
| Length of the diagonal of the cube | $$ \sqrt{3}d \;units \;$$ |
| Length of the diagonal of a face of the cube | $$ \sqrt{2}d \;units$$ |
Characteristics of a Cube
Given below are the main characteristics of a cube.
- A cube is a special case of a rectangular prism where the length, breadth and height are equal in length.
- A cube has six square sides (or faces), twelve edges and eight vertices.
- All the faces of a cube are squares.
- Three sides of the cube meet at each vertex.
- The sides of a cube meet at right angles.
- The opposite edges of a cube are parallel to each other.
- Each vertex of the cube meets three edges and three faces.
- A cube is said to have cubical or octahedral symmetry.
- The main diagonal of a cube passes through the centre of the cube. It is not the same as the diagonal of a face of the cube.
Areas of application
Like most three-dimensional objects, cubes are also seen around us frequently. The most common example is the Rubik’s cube, which is one of the most interesting toys in history. When ice is collected from an ice tray kept in the freezer, we get ice cubes.
Sugar cubes are used as sweeteners for beverages. Rolling dice in several board games are also cubical in shape. Building blocks used by kids are usually in the shape of cubes or cuboids. For special occasions, the gift boxes used are cubical in shape.
We now consider an example making use of the cube formulas.
Question: Each side of a cube has length 8 cm. Find the volume, surface area, length of the main diagonal and length of the diagonal of the face.
Answer: In this problem, the cube has sides of length 8 cm.
Hence, d = 8 cm.
The volume is d3 cm3 = 83 = 512 cm3
Surface area = 6d2 cm2 = 6(8)2 = 384 cm2
Length of the diagonal of the cube = √3 d cm =√3 (8) = 13.86 cm
Length of the diagonal of a face of the cube = √2 d cm = √2 d = 11.31 cm
Question: If the volume occupied by a cube is 1728 cm3, what is the length of each side of the cube?
Answer: The volume of the cube V = 1728 cm3.
Using the formula for the volume of a cube, we find d3 cm3 =1728 cm3
Therefore, to find the length of a side, we need to compute the cube root of the volume.
Hence, d = ∛1728 = 12 cm.
The length of each side of the cube is 12 cm.

