Law of Sines to find the sides and angle.
Law of Sines Calculator
Result:
| Side a: | 0 |
| Side b: | 0 |
| Side c: | 0 |
| Angle ∠A: | 0 |
| Angle ∠B: | 0 |
| Angle ∠C: | 0 |
What is the Law of Sines?
The Law of Sines (or the Sine rule) is the relationship between the sides and angles of a triangle. It states that the ratio of the length of one side of a triangle to the sine of the angle opposite to it, is the same for all the sides and all the angles in that triangle.
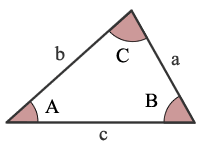
In the triangle shown above;
a, b and c are the lengths of the sides of the triangle, and the angles opposite to them are A, B and C respectively.
Then, the Law of Sines states that
$$ {a\over sin A} = {b\over sin B} = {c \over sin C} $$
Properties of a triangle
Given below are some properties of a triangle.
Perimeter – Total distance covered by the boundary of the triangle.
Area – Region covered by the triangle.
Triangle formulas
Below are the formulas pertaining to a triangle
Perimeter: $$ a+b+c$$
Area (using Heron’s formula): $$ \sqrt{s(s-a)(s-b)(s-c)}$$ where s is the semi-perimeter, s=(a+b+c)/2
Law of sines formulas
The Law of Sines is as follows: $$ {a\over sin A} = {b\over sin B} = {c \over sin C} $$
Below are the formulas to calculate the different Angles:
To find A: $$ {a\over sin A} = {b\over sin B} \;or\; {a\over sin A} = {c \over sin C} $$
Hence, $$ A = sin^{-1}({a \;sin B \over b}) \; or \; A = sin^{-1}({a \;sin C \over c}) $$
To find B: $$ {a\over sin A} = {b\over sin B} \;or\; {b\over sin B} = {c \over sin C} $$
Hence, $$ B = sin^{-1}({b \;sin A \over a}) \; or \; B = sin^{-1}({b \;sin C \over c}) $$
To find C: $$ {a\over sin A} = {c\over sin C} \;or\; {b\over sin B} = {c \over sin C} $$
Hence, $$ C = sin^{-1}({c \;sin A \over a}) \; or \; C = sin^{-1}({c \;sin B \over b}) $$
Below are the formulas to calculate the different Sides:
To find side a: $$ {a\over sin A} = {b\over sin B} \;or\; {a\over sin A} = {c \over sin C} $$
Hence, $$ a = {b \;sin A \over sin B} \; or \; a = {c \;sin A \over sin C} $$
To find side b: $$ {a\over sin A} = {b\over sin B} \;or\; {b\over sin B} = {c \over sin C} $$
Hence, $$ b = {a \;sin B \over sin A} \; or \; b = {c \;sin B \over sin C} $$
To find side c: $$ {c\over sin C} = {b\over sin B} \;or\; {a\over sin A} = {c \over sin C} $$
Hence, $$ c = {b \;sin C \over sin B} \; or \; c = {a \;sin C \over sin A} $$
Areas of application
This law is used to find the lengths of the unknown sides or the unknown angles of the triangle. To find an unknown value, three values must be known.
Let us assume that we want to find the angle A. For this, we need to know the length of the opposite side ‘a’, and another angle-side pair such as angle B and the side b, or angle C and the side c. The calculations follow the side-side-angle (SSA) theorem. The Law of Sines is used for the calculations of the other unknowns. This is because if two sides, and an opposite angle are known, it might just happen that no such triangle exists, leading to an ambiguity.
If we want to find the length of any side, say ‘a’, we need to know the opposite angle A as well as another angle-side pair such as angle B and the side b, or angle C and the side c. These calculations follow the angle-angle-side (AAS) theorem. This is done to avoid cases of ambiguity.
In this section, we consider an example making use of the sine law.
Question: In the triangle below, it is given that A=45⁰, B=60⁰ and the side c=22cm. Find the remaining sides and angle C.
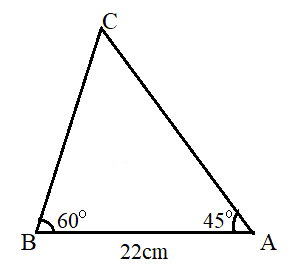
Answer: To find C, we simply use the formula ∠A+∠B+∠C=180°. Therefore, ∠C=180°-45°-60°.We obtain C=75⁰.
By the Law of Sines, $${a\over sin45°} = {b\over 60°} = {22 \over sin 75°}$$
Therefore, $$ a = {22 \; sin 45° \over sin 75°} = 16.11 cm $$
$$ b = {22 \; sin 60° \over sin 75°} = 19.72 cm $$

