Tangent Calculator
Tangent Calculator
Result:
| tan(X): | 0 |
What is tan?
Tan (or tangent) is a trigonometric function. In a right-angled triangle, the tan of an angle x is defined as the ratio of the side opposite to the angle, to the side adjacent to the angle.
$$tan\, x = {opposite \over adjacent}$$
Consider the right-angled triangle below.
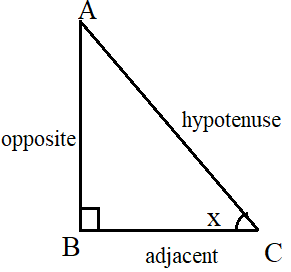
In this triangle, the right angle is at B. We wish to find the tan of x. The side adjacent to the angle x is BC, and the hypotenuse is AC. Therefore,
$$tan\, x\, =\, {opposite \over adjacent} \,=\,{AB\over BC}$$
The tan function may also be written in terms of sin and cos of the angle.
$$tan\, x\, =\, {sin \,x \over cos \,x} $$
Properties of the tan function
Given below are some properties of the tan function.
Angle – Denoted by a variable x or θ, this is the parameter for which the tan value is calculated.
Domain – The values of the angle x for which we can compute tan(x). The tan of an angle x is defined for all values of x, except when x = π/2 + kπ, where k=⋯-1,0,1,… At these points, the denominator of tan(x) is zero, so the function is undefined at these points.
Range – The values between which tan(x) of any angle x lies. This value is – infinitive ≤ tan(x) ≤ +infinitive.
Period – Horizontal length of one complete cycle of the tan function. The period for tan(x) is π radians or 180⁰.
Given below is a graph of the tan function.
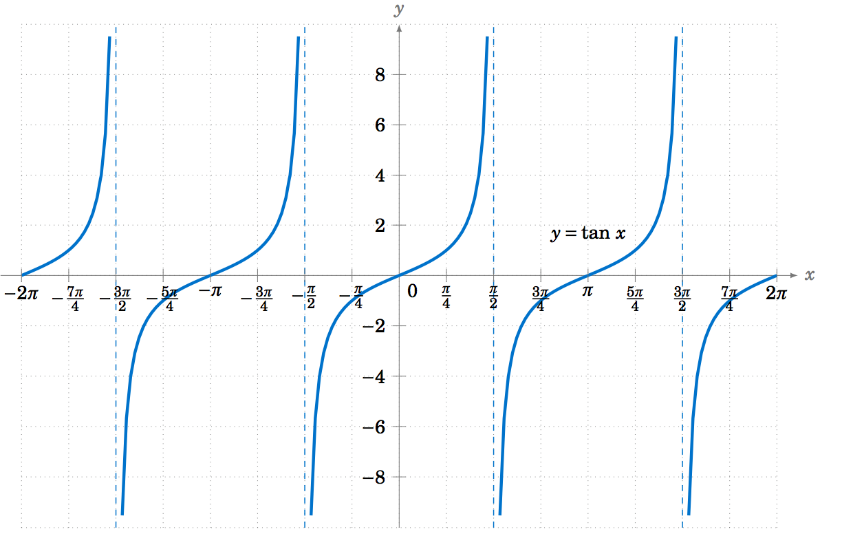
The tan function has a period of π radians (or 180⁰). This means that, the graph repeats itself every π radians. In the above graph, the x axis denotes the angle, and the y-axis denotes tan of that angle.
From the graph, it can be seen that tan(x) starts from 0 and then it keeps increasing. At π/2 radians (or 90⁰), the graph approaches infinity. The same behaviour is observed at 3π/2 radians (or 270⁰).
This can be understood by looking at the definition of tan(x) in terms of sin(x) and cos(x).
$$tan\, x\, =\, {sin \,x \over cos \,x} $$
At x= π/2 radians, sin x=1 and cos x=0. Hence, tanx=1/0, which is undefined.
Values of tan(x)
Given below are some commonly used values of tan(x).
| Angle x in degrees | Angle x in radians | tan(x) |
|---|---|---|
| 0 | 0 | 0 |
| 30 | $$π\over6$$ | $$1 \over √3$$ |
| 45 | $$π\over4$$ | 1 |
| 60 | $$π\over3$$ | √3 |
| 90 | $$π\over2$$ | Not defined |
| 120 | $$2π\over3$$ | -√3 |
| 135 | $$3π\over4$$ | -1 |
| 150 | $$5π\over6$$ | $$-1\over√3$$ |
| 180 | π | 0 |
| 270 | $$3π\over2$$ | Not defined |
| 360 | 2π | 0 |
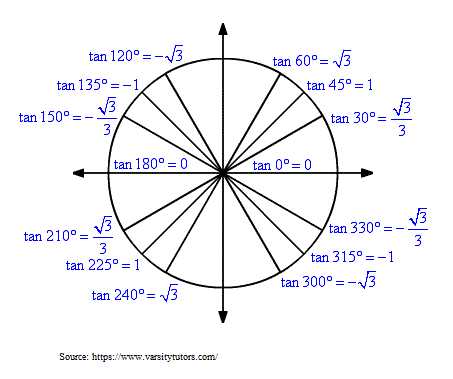
The value of tan(x) can be positive or negative, depending on where the angle x lies in the four quadrants. For example, tan 45⁰ is positive, whereas tan 135⁰ is negative. This has been illustrated below.
| Quadrant | x in degrees | x in radians | Sign of the tan function |
|---|---|---|---|
| 1 | 0⁰ to 90⁰ | $$0\, to\, {π\over2}$$ | + |
| 2 | 90⁰ to 180⁰ | $${π\over2}\, to\, π$$ | - |
| 3 | 180⁰ to 270⁰ | $$π\, to\, {3π\over2}$$ | + |
| 4 | 270⁰ to 360⁰ | $${3π\over2}\, to\, 2π$$ | - |
This unit circle is very useful for determining the values of angles which do not lie between 0 and 2π radians and their signs.
tan formula
To calculate tan(x) from a right-angled triangle, the formula used is;
$$tan\, x = {opposite \over adjacent}$$
The tan of an angle x can also be easily determined if sin(x) and cos(x) are known.
$$tan\, x\, =\, {sin \,x \over cos \,x} $$
Unlike sin(x) and cos(x), there is no well-known Taylor series approximation for tan(x). However, a formula can be obtained by long division as shown below.
$$ tan\, x = {{x = x - {x^3\over3!} + {x^5\over5!} - {x^7\over7!} + {x^9\over9!} - ...} \over {1 - {x^2\over2!} + {x^4\over4!} - {x^6\over6!} + {x^8\over8!} - ...}}$$
This gives the following formula, where x is measured in radians.
$$ tan\, x = x + {x^3\over3} + {2x^5\over15} + ...$$
Areas of application
The tan function is a function of both sin and cos, and these three trigonometric functions are used extensively in science and technology. The most common example is in the study of sound waves or electromagnetic waves.
The tan function is also frequently used in calculus and algebra, and for finding the angles of elevation and depression. The tan function, and formulas involving it, are also frequently used to solve trigonometric problems or prove trigonometric identities.
In this section, we consider some example problems involving the use of the tan function.
Question: A math student is standing 25 feet from the base of a monument. The angle of elevation from her horizontal line of sight is 60⁰. If her height is 5 feet, how tall is the monument?
Answer:This problem can be visualized as below.

The horizontal distance is denoted by BC which is 25 feet. The monument is denoted by AD, which is AB+BD. Here, BD=5 feet indicate the height of the student.
We can find the height of the monument by first using the tan formula and then adding the height of the student.
Hence, AB ≈ 43.3 feet.
Adding the height of the student gives us the height of the monument AD. Here, AD=AB+BD=43.3+5=48.3 feet.
Hence, height of the monument ≈ 48.3 feet.
In the next example, we use the series expansion to find the tan of an angle.
Question: Find the value of tan 25⁰ ?
Answer: For using the series expansion, the angle x must be converted to radians. To convert 25⁰ to radians, we multiply by π and divide by 180.
Angle x in radians = 25π/180 = 0.43633
$$ tan\, x = x + {x^3\over3} + {2x^5\over15} + ...$$
$$ tan\, 0.43633 = 0.43633 + {0.43633^3\over3} + 2x{0.43633^5\over15} + ...$$
tan 0.43633 = 0.43633 + 0.0276905 + 0.0021087 + …
tan 0.43633 = 0.466129
Hence, tan 25⁰ ≈ 0.466
Now, consider the case of an angle which does not lie between 0⁰ and 360⁰.
Question: Find the value of tan 540⁰ ?
Answer: The angle 540⁰ does not lie between 0⁰ and 360⁰. We try to reduce the value of this angle by removing all the full rotations of 360⁰.
Now, 540⁰ = 360⁰ + 180⁰.
Removing one full rotation shows us that tan 540⁰ is equivalent to tan 180⁰.
From the tan graph, as well as the table of listed values, we can see that tan 180⁰ = 0.
Hence, tan 540⁰ = 0.

