Area calculator for 2D Shapes
Area Calculator
Result:
| Area of Circle: | 0 |
Result:
| Area of Rectangle: | 0 |
Result:
| Area of Square: | 0 |
Result:
| Area of Triangle: | 0 |
Result:
| Area of Sector: | 0 |
Result:
| Area of Ellipse: | 0 |
Result:
| Area of Parallelogram: | 0 |
What is an Area?
Area is the quantity which measures the extent of a two-dimensional shape in a plane. In other words, the area of a shape is the region covered by it in a plane.
Area Formulas
Below are the formulas to calculate the areas of different two-dimensional shapes.
Circle
A circle is a closed curve in which all the points on its boundary are at a fixed distance from a given point, which is designated the centre of the circle.
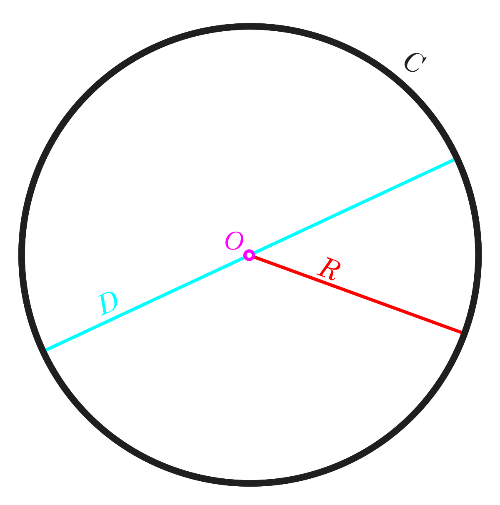
In figure above, O indicates the centre of the circle. The distance between the centre and all the points on the circumference (or the boundary) of the circle is called the radius, marked with R.
The area of the circle is calculated by the formula: πr2 square units
Rectangle
A rectangle is a polygon having four sides and four vertices, and the angle at each vertex is a right angle. The opposite sides of a rectangle are equal in length and parallel to each other. A rectangle has a specific length and width, which are different from each other.
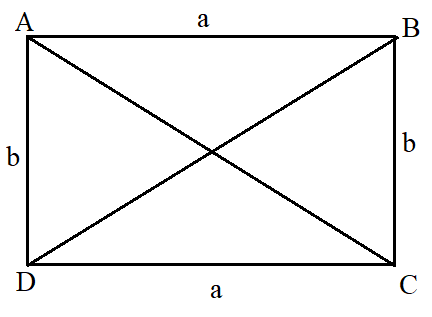
In this figure, the sides AB = CD = a (length of the rectangle), and AD = BC = b (width). The area is calculated as ab square units
Square
A square is a special case of a rectangle in which all the sides are equal in length.
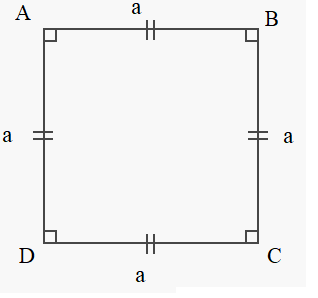
The figure above shows a square where the length of the side is ‘a’ units. Hence, the area is a2 square units.
Triangle
A triangle is a polygon having three vertices and three edges. Depending on their sides, triangles are of three types.
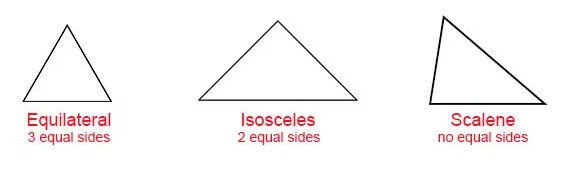
- An equilateral triangle is one which all the sides are equal in length.
- An isosceles triangle has exactly two sides equal in length.
- A scalene triangle is a triangle where the three sides are of different lengths.
The figure below describes the three types of triangles.
.
The formula for the area of a triangle is $$ \sqrt{s(s-a)(s-b)(s-c)} \;square \;units$$ where 's' is the semi-perimeter, $$ s \; = \; {a+b+c}\over 2 $$and a, b and c indicate the lengths of the three sides.
For a right-angled triangle, the area can be calculated as $$ {1\over2}ab \;square \;units,$$ where a and b are the sides of the triangle other than the hypotenuse.
Sector
A sector is the region of a circle bounded by two radii of the circle, and the arc in between. The arc is a small part of the circumference, and the radii are the endpoints of this arc.
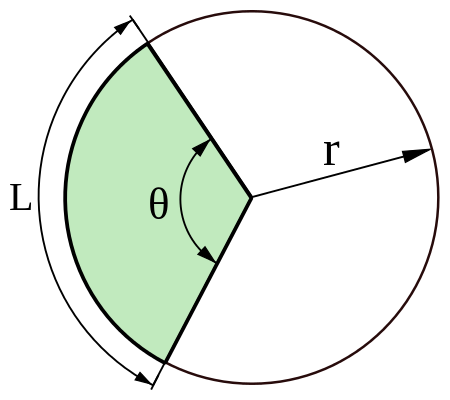
Given above is the figure of a sector. In this figure, θ denotes the angle made by the sector at the centre of the circle, r is the radius and L is the arc length. The area of a sector is the sum of the arc length and the two radii.
The formula is $$r^2 \,{θ\over2} \;square \;units \;(if \,θ \,is \,in \,radians) \\or \\πr^2\, {θ⁰\over360⁰} \;square \;units \;(if \,θ \,is \,in \,degrees).$$
Ellipse
An ellipse is the set of all points in a plane such that the sum of their distances from two fixed points in the plane is a constant. These two fixed points are known as the foci of the ellipse. Given below is a figure of an ellipse.
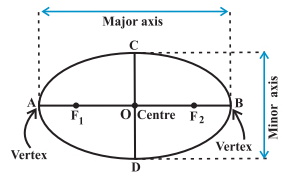
In this figure, the two foci are F1 and F2. The ellipse is defined by its axes. The major axis of the ellipse is the longest diameter of the ellipse, and the minor axis is the smallest diameter. In the figure above, AB is the major axis, which is usually denoted by ‘a’ and CD is the minor axis, denoted by ‘b’.
The area of an ellipse is πab square units.
Parallelogram
A parallelogram is a polygon having four sides and four vertices, and in which the opposite sides are parallel to each other and equal in length. This has been shown in the figure below.
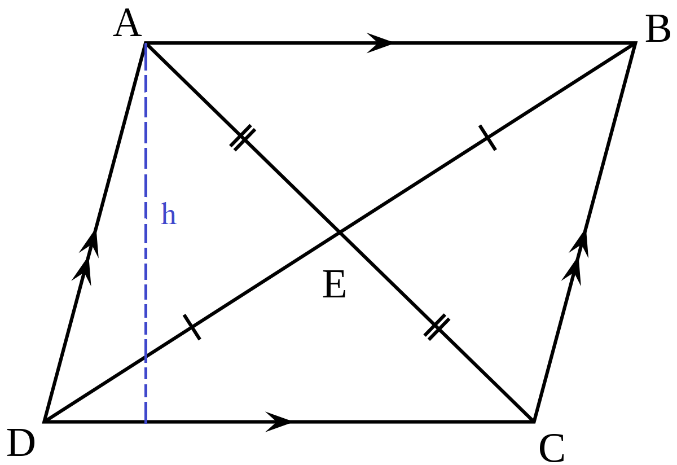
ABCD is a parallelogram where the sides AB = CD = b, and AD = BC = a. Moreover, AB is parallel to CD, and AD is parallel to BC. The height h has been marked with a blue line.
The area is calculated as $$bh \;square \;units \\ or \\ a \,b \,sinA \;square \;units \\ or \\ a \,b \,sinB \;square \;units, $$ where A and B are the angles at the vertices A and B respectively.
Areas of application
The area formulas are very important in mathematics, especially geometry and calculus. Using the well-known formulas of areas for simple shapes, the area of any polygon can be found. For shapes with irregular boundaries, calculus is used to find the area. This can also be done by dividing the curve into some small rectangles and estimating the area of each. A real-life example is the construction of a house. As we need to pour concrete in the foundation, within the constraints of the house, the area would have to be maximized which is related to the perimeter of the constraints.

