Right Angle Triangle Calculator
Right Angle Triangle Calculator
Result:
| Side a: | 0 |
| Side b: | 0 |
| Side c: | 0 |
| Angle ∠A: | 0 |
| Angle ∠B: | 0 |
| Angle ∠C: | 0 |
What is a right-angled triangle?
A right-angled triangle (or a right triangle) is a triangle where one of the angles measure 90⁰. The relationships between the angles and sides of a right-angled triangle constitute the framework for trigonometry.
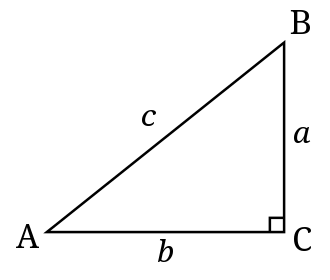
In the right-angled triangle shown above;
The right angle is at C. The side opposite the right angle is called the hypotenuse, which is side ‘c’ in this figure. The sides adjacent to the right angle are called its legs. The side opposite ∠A is identified as side ‘a’, and the one opposite ∠B is identified as side ‘b’.
If two of the sides of a right-angled triangle are known, the third side can be measured using the Pythagoras theorem. This theorem states the square of the hypotenuse is equal to the sums of the squares of the other two sides, that is, a2+b2=c2.
Properties of a right-angled triangle
Given below are some properties of a right-angled triangle.
Hypotenuse – The side opposite the right angle.
Perimeter – Total distance covered by the boundary of the triangle.
Area – Region covered by the right-angled triangle.
Altitude - The perpendicular drawn from the vertex containing the right angle to the hypotenuse. The figure below shows the right-angled triangle with the altitude f.
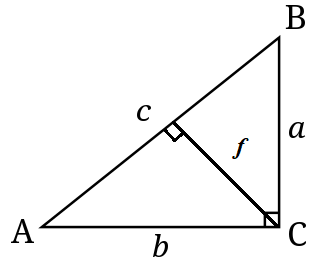
The altitude divides the triangle into two smaller triangles which are similar to each other and the bigger triangle. Hence, this gives us three similar triangles.
Right-angled triangle formulas
Below are the formulas pertaining to a right-angled triangle
Pythagoras Theorem: $$ {a^2} + {b^2} = {c^2}$$
Area: $$ {1\over2}ab$$
Perimeter: $$ a+b+c$$
Area (using Heron’s formula): $$ \sqrt{s(s-a)(s-b)(s-c)}$$ where s is the semi-perimeter, s=(a+b+c)/2
Length of the altitude: $$ {1\over a^2}+{1\over b^2}={1\over f^2}$$ where f denotes the altitude.
Side b (when a and c are known): $$ b = \sqrt{c^2-a^2}$$
Side c (when a and b are known): $$ c = \sqrt{a^2+b^2}$$
Side a (when a and c are known): $$ a = \sqrt{c^2-b^2}$$
Angle A: $$ sin^{-1}({a\over c})$$
Angle B: $$ sin^{-1}({b\over c})$$
For the angle A:
$$ sin A = {a\over c} \;or\; ∠A = sin^{-1}({a\over c})$$
$$ cos A = {b\over c} \;or\; ∠A = cos^{-1}({b\over c})$$
$$ tan A = {a\over b} \;or\; ∠A = tan^{-1}({a\over b})$$
$$ cosec A = {c\over a} \;or\; ∠A = cosec^{-1}({c\over a})$$
$$ sec A = {c\over b} \;or\; ∠A = sec^{-1}({c\over b})$$
$$ cot A = {b\over a} \;or\; ∠A = cot^{-1}({b\over a})$$
For the angle B:
$$ sin B = {b\over c} \;or\; ∠B = sin^{-1}({b\over c})$$
$$ cos B = {a\over c} \;or\; ∠B = cos^{-1}({a\over c})$$
$$ tan B = {b\over a} \;or\; ∠B = tan^{-1}({b\over a})$$
$$ cosec B = {c\over b} \;or\; ∠B = cosec^{-1}({c\over b})$$
$$ sec B = {c\over a} \;or\; ∠B = sec^{-1}({c\over a})$$
$$ cot B = {a\over b} \;or\; ∠B = cot^{-1}({a\over b})$$
Characteristics of a right-angled triangle
Given below are the main characteristics of a right-angled triangle.
- One of the angles is 90⁰.
- The side opposite the 90⁰ angle is called the hypotenuse. It is the longest side of the triangle.
- The sum of the three angles is 180⁰.
- The angles A and B are complementary to each other, that is, ∠A+∠B=90°
- The altitude gives rise to three similar triangles.
- The area of the triangle can be calculated from the lengths of the sides adjacent to the right angle.
- If the angles ∠A=∠B=45°, then the triangle is an isosceles right-angled triangle. In that case, the sides ‘a’ and ‘b’ will be equal in length.
- A triangle cannot have 2 right angles. Otherwise, the sum of two of the angles will be 180⁰ and the third angle would be 0, which is not possible
Areas of application
Right-angled triangles are used in trigonometry to find relationships between the sides and angles of the triangle. These trigonometric relations find applications in various branches of mathematics, science and engineering.
Consider the following examples:
Question: A person standing some distance away from the foot of a flagpole finds that his line of sight of top of the tower is making an angle of 30⁰ with the horizontal. If the height of the pole is 10 metres, how far away is the person standing?
Answer: The problem can be visualized as below.
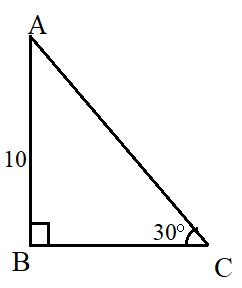
Here, height of the flagpole AB = 10 metres.
Angle of elevation = 30⁰
We need to find BC which is the distance of the person from the pole. For this, we can use the cos formula.
$$ cos\, 30° = {opposite\over adjacent} = {10\over BC}$$
$$ {\sqrt3 \over 2} = {10\over BC}$$
$$ BC = {{10 x 2}\over \sqrt 3} ≈ 11.55 metres$$
Hence, the person is standing 11.55 metres away from the flagpole.
Question: Find the length of the hypotenuse and area of the triangle when it is given that two of the sides measure 8cm and 6cm.
Answer: It is given that the two sides of a right-angled triangle measure 8cm and 6cm.
Therefore, a=8cm and b=6cm.
The hypotenuse c can be calculated from the Pythagoras theorem,
$$ c = \sqrt{{a^2+b^2}} = \sqrt{8^2 + 6^2} $$
Hence, c=√100=10cm.
Area of the triangle = 1/2 ab=1/2×8×6=24 cm2.

