Mixed Fraction Comparison - Compare two mixed fraction numbers and find the relation between the two.
Mixed Fraction Comparison
Input Number 1
Input Number 2
Fraction number operations:
| Operation | Result |
| Number 1: | 0 |
| Number 2: | 0 |
|
|
0 |
What is a Fraction?
In mathematics, a fraction is a number of the form a/b, where b ≠ 0. It represents some part of a whole.
The part ‘a’ above the dividing line is called the numerator of a fraction, and the part below ‘b’ is called a denominator.
In most cases, the numerator and denominator are both integers. The denominator denotes the total number of parts which comprise the whole, and the numerator denotes the number of parts of the total.
Consider the example below of a pizza cut into 4 slices.
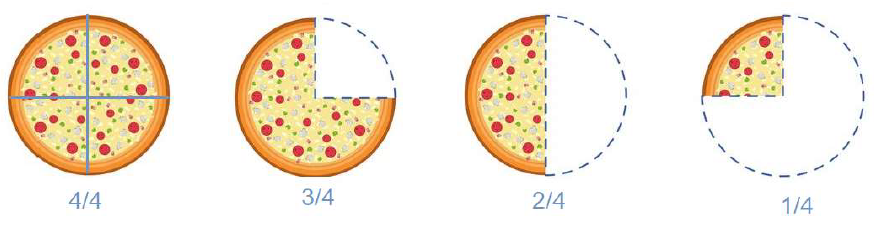
When all four slices of the pizza are present, the fraction is written as 4/4. The 4 in the denominator indicates that 4 slices make up the whole pizza.
When one slice of the pizza has been eaten, 3 slices remain which is indicated by the fraction ¾. The numerator 3 indicates the number of parts of the total 4 slices.
When 2 slices are eaten, 2 slices remain, indicated by 2/4. Finally, when only one slice remains, it is represented by ¼.
Comparison of fractions refers to checking which fraction is greater then, lesser than or equal to the other one. We now try to compare the four fractions obtained above. To begin the comparison, the first thing we need to ensure is that the denominators are the same. The next thing we do, is compare the numerators. Clearly, among the numerators, 4 is the greatest and 1 is the least. Hence, we obtain the relation,
$$ {4\over4} < {3\over4} <{2\over4} < {1\over 4} $$
Once the fractions are reduced to their simplest form, this can be written as $$ 1 < {3\over 4} < {1\over 2} < {1\over 4} $$
Comparing proper and improper fractions
If the fractions have like denominators, comparing them becomes quite easy as we only need to check the numerators. In case the fractions have unlike denominators, the steps followed are given below. For this, we consider the fractions 5/6 and 9/8.
1) First, we find the least common multiple (LCM) of the denominators. The LCM of 6 and 8 is 24.
2) Now we convert each fraction into an equivalent fraction by multiplying with the number, which gives the LCM when it is multiplied with the denominator.
Therefore, 6 is multiplied by 4 and 8 is multiplied by 3. $$ {{5*4}\over{6*4}} = {20\over24} \; and \; {{9*3}\over{8*3}} = {27\over24} $$
3) Now, we compare the numerators. Clearly, 27 is greater than 20. Therefore, $$ {5\over6}<{9\over8} $$
Comparing a proper/improper fraction and a mixed fraction
For comparing mixed fractions, or a mixed fraction and an improper (or proper) fraction, an extra step needs to be done. For this, we consider the fractions, 5/6 and a𝑛𝑑 1 (5/8).
1) We first convert the mixed fraction to an improper fraction. 1 5/8 as an improper fraction is 13/8.
2) Now we find the least common multiple (LCM) of the denominators. The LCM of 6 and 8 is 24.
3) We convert each fraction into an equivalent fraction by multiplying with the number, which gives the LCM when it is multiplied with the denominator.
Therefore, 6 is multiplied by 4 and 8 is multiplied by 3. $$ {{5*4}\over{6*4}} = {20\over24} \; and \; {{13*3}\over{8*3}} = {39\over24} $$
4) Now, we compare the numerators. Clearly, 27 is greater than 20. Therefore, $$ {5\over6} < 1 {5\over8} $$
Comparing two mixed fractions
When both the fractions are mixed fractions, the steps are slightly different.
i) If the whole numbers of the mixed fractions are the same, we only compare the fractional part.
ii) If the whole numbers are different, we compare only the whole numbers. The fraction with the bigger whole number is bigger.
Consider an example where the fractions have the same whole number. We now compare 2 5/6 𝑎𝑛𝑑 2 3/8.
1) As the whole number is the same, we only consider the fractions 5/6 𝑎𝑛𝑑 3/8.
2) The LCM of 6 and 8 is 24. So, the first fraction is multiplied by 4 and the second fraction is multiplied by 3. $$ {{5*4}\over{6*4}} = {20\over24} \; and \; {{3*3}\over{8*3}} = {9\over24} $$
3) On comparing the numerators, we find that 20 is greater than 9. Therefore, $$ 2{5\over6} > 2 {3\over8} $$
Consider another example of mixed fractions where the whole number is different. We now compare 2 5/6 𝑎𝑛𝑑 3 1/8. As the second fraction has a larger whole number, it is larger than the first one. $$ 2{5\over6} < 3{1\over8} $$
Areas of application
Comparison of fractions is very useful when we need to compare quantities. Consider the following problem.
Question: Michael and Jim bought some chocolates from two different stores for the same price, $10. Michael bought 3 4/7 pounds of chocolate, whereas Jim bought 3 2/5 pounds. Who had to spend more?
Answer: Even though Michael and Jim spent the same amount of money, we need to compare the quantities of chocolate to estimate who had to spend more.
As the whole number of both the fractions is the same, we need to compare only the fractional parts. We only consider the fractions 4/7 𝑎𝑛𝑑 2/5.
The LCM of 7 and 5 is 35. So, the first fraction is multiplied by 5 and the second fraction is multiplied by 7. $$ {{4*5}\over{7*5}} = {20\over35} \; and \; {{2*7}\over{5*7}} = {14\over35} $$
On comparing the numerators, we find that 20 is greater than 9. Therefore, $$ 3{4\over7} > 3{2\over5} $$
Even though both of them spent $10 on the chocolate, the quantity purchased by Jim is lesser than Michael’s. Therefore, Jim had to spend more.

