Calculate the volume of the cone, surface area of the cone and know the formulas.
Cone Calculator
Result:
| Radius: | 0 |
| Height: | 0 |
| Volume: | 0 |
| Surface Area: | 0 |
What is a Cone?
In three-dimensional geometry, a cone is a shape which becomes narrower smoothly from a flat base (sometimes, circular) to a point called the apex or vertex. A cone is formed from line segments, lines or half-lines connecting a common point, the vertex, to all the points on the base. A cone can also be defined as a pyramid with a circular cross-section, unlike pyramids which have a triangular cross-section. Such cones are called circular cones.
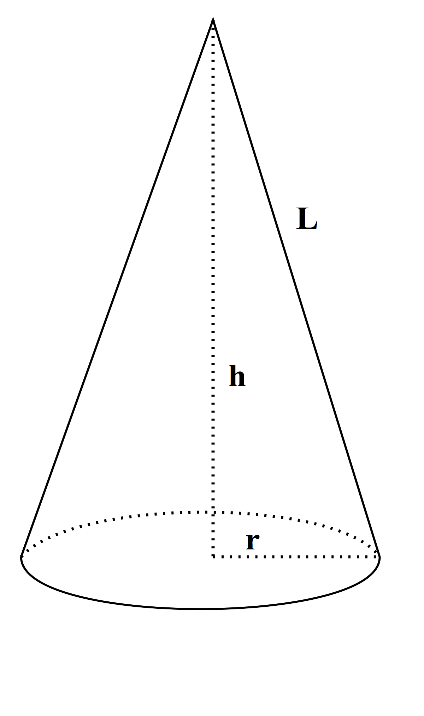
In the above figure, the base of the cone is a circle of radius r. The distance from the centre of the base to the vertex of the cone is called the height h of the cone. The distance from the vertex to any point on the circumference of the base is called the slant height of the cone indicated by L.
Properties of Cone
Given below are some properties of a cone.
Slant height – The distance from the vertex to any point on the circumference of the base, via a line segment, is called the slant height of the cone.
Volume – This is the total space occupied by the cone.
Lateral surface area – The lateral surface area of a cone is the area of the cone excluding the surface area of the base.
Surface area – Surface area is the total area covered by the cone. It is equal to the sum of the lateral surface area and the area covered by the circular base.
Cone formulas
Given below are the formulas of a cone.
| Volume | $$ {1\over3}πr^2h \;cubic \,units $$ |
| Lateral surface area | $$ πr \, \sqrt{r^2+h^2} \;square \;units \;$$ |
| Surface area | $$ πr^2 \; + \; πr \, \sqrt{r^2+h^2} \;square \;units \;$$ |
| Slant Height | $$ \sqrt{r^2+h^2} \;square \;units$$ |
Characteristics of a Cone
Given below are the main characteristics of a cone.
- A cone has one vertex (or apex), and one face (which is the circle at the base).
- It does not have any edges.
- A cone is also defined as a pyramid with a circular cross-section.
- The slant height of a cone is the distance from the vertex to any point on the circumference of the base, via a line segment.
- If a cone has a circular base, and the axis from the vertex to the base passes through the centre of the circle at the base, then the cone is said to be a right cone. In such a cone, the vertex lies just above the centre of the circular base.
- In a right cone, the axis and the base of the cone form a right angle.
- If a cone has a circular base, but the axis of the cone is not perpendicular to the base, then the cone is said to be an oblique cone.
- In an oblique cone, the vertex of the cone does not lie just above the circle at the base. This is why the cone looks tilted.
The figure below shows the two types of cones.

Areas of application
Cones are frequently observed all around us, such as wafer cones used to scoop ice cream into. Birthday hats are also conical. Traffic cones, like the orange and white coloured ones seen on the roads and occasionally in playing arenas, are also cones.
Funnels are also shaped as cones: they have a broad mouth on top and a narrow opening below. They are used to filter liquids. Conical shapes can also be observed in buildings, such as caste turrets and temple tops. Vegetables like carrots and radish are also conical in shape. When a pencil is sharpened, the tip of the pencil is in the shape of a cone. Even the Christmas tree is in the shape of a cone.
We now consider a real-life example making use of the cone formulas.
Question: A conical storage tank, 9 feet high and 14 feet wide, is used for storing water. What is the maximum amount of water this tank can hold? If the exterior of the tank is to be painted, what would be the total area of the tank required to paint?
Answer: According to the question, the storage tank is 14 feet wide. This indicates the diameter of the circle at the base.
Hence, the radius of the base r = 7 feet.
Height of the tank, h = 9 feet.
Quantity of water it can hold can be measured by its volume $$ V \; = \;{1\over3}πr^2h $$
Therefore, $$ V\;=\;{1\over3} \,π(7^2)9 \; = \; {1\over3} \,π×49×9 = 461.81 \;cubic \;feet$$
To find the area to be painted, we need to compute the total surface area of the tank.
Surface area = $$ πr^2 \;+ \; πr \,\sqrt{r^2+h^2} \;square \;feet \\ π(7)^2 \,+ \,π×7 \sqrt{7^2+9^2} \; square \;feet \\ π×49 \;+ \;π×7×12 \; = \;49π+84π \;= \;133π \; square\; feet$$
Hence, the total surface area = 133π = 417.832 square feet.
So, the volume of water this tank can hold is nearly 461.81 cubic feet, and the total area to be painted is 417.832 square feet.

