Fraction Simplifier - reduce the fraction number
Fraction Simplifier
Fraction Number
Result Summary:
| Type | Result |
| Given Fraction number | 0 |
| Simplified Fraction number | 0 |
What is a Fraction?
In mathematics, a fraction is a number of the form a/b, where b ≠ 0. It represents some part of a whole.
The part ‘a’ above the dividing line is called the numerator of a fraction, and the part below ‘b’ is called a denominator.
In most cases, the numerator and denominator are both integers. The denominator denotes the total number of parts which comprise the whole, and the numerator denotes the number of parts of the total.
Consider the example below of a pizza cut into 4 slices.
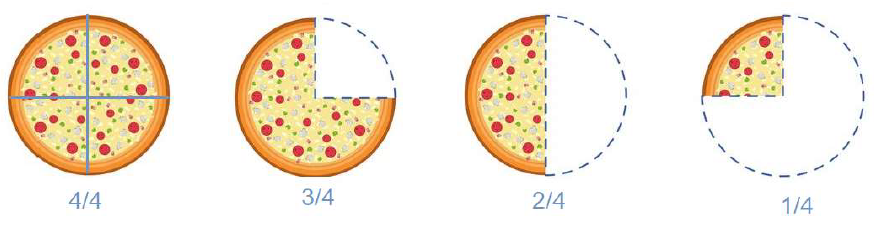
When all four slices of the pizza are present, the fraction is written as 4/4. The 4 in the denominator indicates that 4 slices make up the whole pizza.
When one slice of the pizza has been eaten, 3 slices remain which is indicated by the fraction ¾. The numerator 3 indicates the number of parts of the total 4 slices.
When 2 slices are eaten, 2 slices remain, indicated by 2/4. Finally, when only one slice remains, it is represented by ¼.
In the third image, 2/4 is the fraction of the pizza left. This can be simplified further. For doing so, we need to find a common factor between the numerator and denominator. Here, 2 is the common factor. Therefore, 2/4 can be written as ½.
Properties of fractions
Given below are some important properties of fractions.
Numerator – The number which is above the dividing line of a fraction.
Denominator – The number which is below the dividing line of a fraction.
Commutative property – The addition and multiplication of fractions is commutative. This implies that, the order in which these fractions are written does not matter: the final answer is the same. $$ {a\over b}+{c\over d} = {c\over d} + {a\over b} \; and \; {a\over b}*{c\over d} = {c\over d} * {a\over b} $$
Associative property – The grouping of fractions for addition and multiplication does not affect the final answer. Hence, fraction addition and multiplication are associative. $$ ({a\over b}+{c\over d})+{e\over f} = {a\over b} + ({c\over d} + {e\over f}) \; and \; ({a\over b} * {c\over d}) * {e\over f} = {a\over b} * ({c\over d} * {e\over f}) $$
Distributive property – The multiplication of a fraction over the addition of two or more fractions gets distributed. This means the following. $$ {a\over b}*({c\over d} + {e\over f}) = ({a\over b}*{c\over d}) + ({a\over b}*{e\over f}) $$
Identity property – The additive identity of any fraction is 0. This means that, when 0 is added to any fraction, we get back the fraction itself. The multiplicative identity of a fraction is 1. Therefore, 1 multiplied by any fraction gives back the original fraction. $$ {a\over b}+0 = 0+{a\over b} = {a\over b} \; and \; {a\over b} *1 \; = \; 1*{a\over b} = {a\over b} $$
Inverse property – The inverse of any fraction is its reciprocal. The reciprocal of a fraction is another fraction where the positions of the numerator and denominator are interchanged. When a fraction is multiplied by its reciprocal, the result is 1. $$ {a\over b}*{b\over a} = 1 $$
The fraction b/a is known as the reciprocal (or multiplicative inverse) of the fraction a/b.
Equivalent fractions
It is often more convenient to work with fractions that have been simplified to their lowest terms. This is known as reducing a fraction.
For example, consider the fraction 20/40. This fraction can be reduced further to a fraction with a smaller numerator and denominator. We try to do this by dividing the numerator and denominator repeatedly with some numbers until we come to a point where the fraction cannot be simplified further.
20 divided by 10 is 2. 40 divided by 10 is 4. So, this fraction can now be written as 2/4. However, 2/4 is still not the simplest form. 2 and 4 can be divided further by 2 to obtain ½. The fraction ½ is now in its simplest form because it cannot be reduced further.
As the fractions 20/40, 2/4 and ½ indicate the same fraction after reducing it to lowest terms, they are known as equivalent fractions. Although all the three fractions are the same, for computational purposes, it helps to reduce the fraction to its simplest form.
Now consider the fraction 5/12. It is not possible to find a number which divides both 5 and 12 simultaneously. Hence, the fraction 5/12 in its lowest form.
Steps for simplifying fractions
Fractions can be simplified easily by repeated division of common factors or by finding the GCD. The latter has been described in the steps below.
For example, in the case of 20/40. The GCD of 20 and 40 is 20. On dividing the numerator and denominator by 20 and 40, we get ½, which is the simplest form of the fraction.
In the case of 5/12, the GCD of 5 and 12 is 1. Hence, this fraction is in its simplest form and cannot be reduced further.
Areas of application
Some of the real-world applications of simplifying fractions are:
1) Dividing a pizza or pie into equal slices involves cutting it up into a number of fractions which make up the whole pizza (or pie). When 6 out of 8 slices of a pizza remain, we denote this by 6/8. On reducing this fraction, we obtain ¾. Hence, ¾ of the pizza remains.
2) In examinations, grades are assigned according to the marks obtained out of the total marks for the exam. For example, a score of 14/20 indicates that the person scored 14 marks out of the total 20. 14/20 can be reduced further to 7/10.
3) When we go shopping and find something on discount, there is a deduction on the original price which is calculated using fractions. For example, if a dress worth INR 1000 is available on 40% discount, the new price of the dress is 1000 – 40% of 1000 = INR 600. 40% of the original price is 40/100 of 1000. 40/100 is essentially 2/5, hence 40% discount on 1000 indicates a discount of INR 400.

