Pythagorean theorem
Pythagorean theorem Calculator
Result:
| Hypotenuse c: | 0 |
Result:
| Side a: | 0 |
Result:
| Side b: | 0 |
What is a Pythagoras theorem?
The Pythagoras theorem is a very important concept in mathematics, particularly geometry and trigonometry. It gives the relation between the sides of a right-angled triangle. A right-angled triangle is one where one of the angles measure 90⁰. The Pythagoras theorem helps us to find the length of an unknown side of the triangle, when the lengths of the other two sides are known.
Consider the right-angled triangle below.
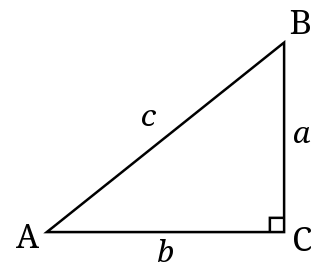
Here, the right angle is at C. The side opposite the right angle is called the hypotenuse, which is side ‘c’ in this figure. The sides adjacent to the right angle are called its legs. The side opposite ∠A is identified as side ‘a’, and the one opposite ∠B is identified as side ‘b’.
If two of the sides of a right-angled triangle are known, the third side can be measured using the Pythagoras theorem. This theorem states the square of the hypotenuse is equal to the sums of the squares of the other two sides, that is, a2 + b2 = c2.
Properties of a right-angled triangle
Given below are some properties of a right-angled triangle.
Hypotenuse – The side opposite the right angle.
Perimeter – Total distance covered by the boundary of the triangle.
Area – Region covered by the right-angled triangle.
Pythagoras theorem and right-angled triangle formulas
Below are the formulas pertaining to a right-angled triangle.
| Pythagoras Theorem | $$ a^2 \;+ \;b^2 \; = \;c^2 $$ |
| Side b (when a and c are known) | $$ b \;= \; \sqrt{c^2-a^2} $$ |
| Side c (when a and b are known) | $$ c \;= \; \sqrt{a^2+b^2} $$ |
| Side a (when c and b are known) | $$ a \;= \; \sqrt{c^2-b^2} $$ |
| Area of the right-angled triangle | $$ {1\over2} \, ab $$ |
| Area (using Heron’s formula) | $$ \sqrt{s(s-a)(s-b)(s-c)} \;square \;units$$ where 's' is the semi-perimeter, $$ s \; = \; {{a+b+c}\over 2} $$ |
| Perimeter | $$ a+b+c $$ |
Areas of application
The Pythagoras theorem can be used to determine the length of the missing side of a right-angled triangle. If any two of the sides are known, the third side can be calculated quite easily. In rectangles and squares, the Pythagoras theorem can be used to find the lengths of the diagonal. It can also be used to determine if a given triangle is right-angled or not.
It also has several real-life applications. Televisions and monitor screens are always measured in terms of the diagonal. When buying these products, the size is an indication of the length of the diagonal. For example, a 40-inch TV screen has a diagonal length of 40 inches, which can be determined using the length and width of the screen. The Pythagoras theorem is also used for two-dimensional navigation. The distances north and west may indicate the two legs of a right-angled triangle, and the shortest line connecting them is the diagonal.
We consider some examples making use of the Pythagoras theorem.
Question: A triangle with lengths 20 cm, 21 cm and 29 cm is given. Determine if this triangle is right-angled or not.
Answer: The problem considers a triangle having lengths 20 cm, 21 cm and 29 cm. The side measuring 29 cm is the longest. It also satisfies the condition 20 + 21 > 29.
We know that a2 + b2 = c2.
We assume a = 20 cm, b =21 cm and c = 29 cm.
Now, a2 + b2 = 202 + 212 = 841. Moreover, c2 = 292 = 841.
Hence, in this triangle, a2 + b2 = c2 is satisfied. Therefore, the given triangle is right-angled.
Question: Find the length of the hypotenuse and area of the triangle when it is given that two of the sides measure 9 cm and 12 cm.
Answer: Consider the right-angled triangle below.
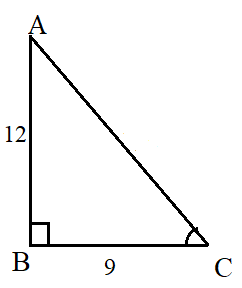
Two of the sides have been marked as BC = 9 cm, and AB = 12 cm.
The hypotenuse AC can be calculated from the Pythagoras theorem, $$ c \; = \; \sqrt{a^2+b^2} \; = \; \sqrt{12^2+9^2} $$
Hence, $$ c \; = \; \sqrt{125} \; = \; 15 \; cm $$
Area of the triangle is $$ {1\over2} ab \; = \; {1\over2}*9*12 \; = \; 54 \; cm^2 $$

