Parallelogram calculator
Parallelogram Calculator
Result:
| Perimeter of parallelogram: | 0 |
| Area of parallelogram: | 0 |
| Diagonal of parallelogram: | 0 |
What is a parallelogram?
In two-dimensional geometry, a parallelogram is a polygon having four sides and four vertices, and in which the opposite sides are parallel to each other and equal in length. This has been shown in the figure below.
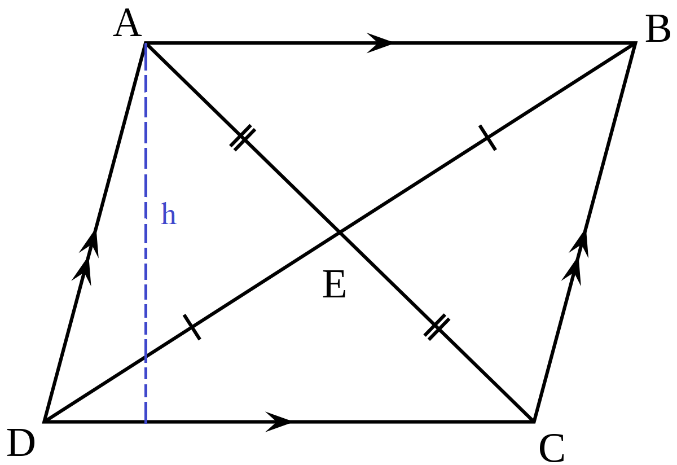
ABCD is a parallelogram where the sides AB = CD, and AD = BC, that is, the opposite sides are equal. Moreover, AB is parallel to CD, and AD is parallel to BC. The blue dotted line indicates the height of the parallelogram.
The opposite angles of the parallelogram are equal. So, angle A = angle C, and angle B = angle D. The sum of these four angles is 360⁰. The two diagonals of the parallelogram are AC and BD. They bisect each other at the point E.
Properties of a parallelogram
Given below are some properties of a parallelogram.
Area – Region covered by the parallelogram.
Perimeter – Total distance covered by the boundary of the parallelogram.
Diagonal – The line segments connecting the opposite vertices of a parallelogram. In the figure above, the diagonals are AC and BD.
A parallelogram is a quadrilateral with opposite sides equal and parallel. There are different kinds of parallelograms as shown below.
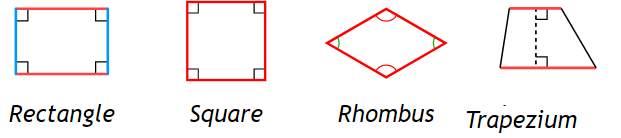
Rectangle – A rectangle is a parallelogram with opposite sides equal and parallel, and where each interior angle measures 90⁰. The diagonals are also equal in length.
Square – A square is a special case of a rectangle in which all the sides are equal in length. Each interior angle measures 90⁰, and the diagonals are also equal in length.
Rhombus – This is a parallelogram in which all sides are equal, and the opposite sides are equal. The diagonals in a rhombus bisect each other at 90⁰.
Trapezium – A trapezium is a kind of quadrilateral where there is one pair of parallel sides, and the other two sides are non-parallel.
Parallelogram formulas
Below are the formulas to calculate different properties of a parallelogram. Here, ‘a’ denotes the length of the slant side (AD and BC), ‘b’ is the length of the base (DC = AB) and h is the height of the parallelogram.
| Area | $$bh \;square \;units \\ or \\ a \,b \,sinA \;square \;units \\ or \\ a \,b \,sinB \;square \;units, $$ where A and B are the angles at the vertices A and B respectively. |
| Perimeter | $$ 2(a+b) units $$ |
| Length of the diagonal | $$ \sqrt{(b^2+a^2+2ba cosθ )} \;units,$$ where θ is the angle between the base and the slant side. |
Characteristics of a Parallelogram
Given below are the main characteristics of a parallelogram.
- A parallelogram is a four-sided polygon where the opposite sides are equal and parallel.
- The sum of the angles in a parallelogram is 360⁰.
- The opposite angles are equal.
- The sum of the angles which lie on the same side is 180⁰. This means that, angle A + angle D = 180⁰, and angle C + angle B = 180⁰.
- The diagonals bisect each other.
- The diagonals divide the parallelogram into congruent triangles.
Areas of application
Some real-life examples of parallelograms include books, letters, tables, and the arrangement of streets on a map, sheets of paper, stamps, building blocks and many more. The Dockland office building in Hamburg, Germany is an example of a parallelogram, which is neither a square, rectangle nor rhombus.
We now observe an example using the parallelogram formulas.
Question: The base and slant side of a parallelogram are 2.6 cm and 2.3 cm respectively. The angles A and B measure 60⁰ and 120⁰ respectively. Find the area, perimeter and lengths of the diagonals.
Answer: The parallelogram can be drawn as shown below.
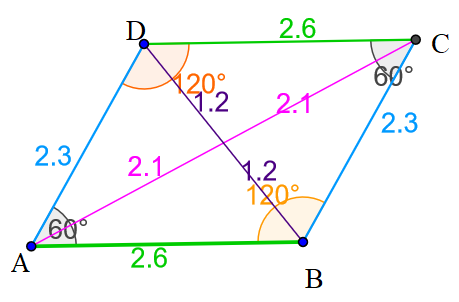
Here, AB = CD = b = 2.6 cm, and AD = BC = 2.3 cm
| Perimeter: | $$ 2(a+b) \;cm \;= \;2(2.3+2.6) \;cm \;= \;9.8 \;cm $$ |
| Area: | $$ a \,b \,sinA \;cm^2 \;= \;2.3×2.6×sin60 \;= \;4.58 \;cm^2 $$ |
| Length of the diagonal AC : | $$ = \; \sqrt{b^2+a^2+2ba \,cosθ} \\ = \; \sqrt{2.6^2+2.3^2+2×2.6×2.3 \,cos60} \\ = \; \sqrt{6.76+5.29+5.98} \; = \sqrt{18.03} \; ≈ \;4.2 \;cm$$ |
| Length of the diagonal BD : | $$ = \; \sqrt{b^2+a^2-2ba \,cosθ} \\ = \; \sqrt{2.6^2+2.3^2-2×2.6×2.3 \,cos60} \\ = \; \sqrt{6.76+5.29-5.98} \; = \sqrt{6.07} \; ≈ \;2.4 \;cm$$ |
Hence, area of the parallelogram is 4.58 cm2, the perimeter is 9.8 cm, and the lengths of the two diagonals are 4.2 cm and 2.4 cm.

