Calculate the addition of two numbers:

Addition Calculator



Result:

X + Y: 0


What is Addition?

Addition is one of the basic arithmetic operations. It involves taking two (or more) numbers, and combining them to get a new number. This new number is called the sum of the numbers which were added. The symbol used to denote addition is “+”, called the plus sign. The numbers which are being added together are called addends, and the number obtained after addition is called the sum.


For example, consider “4 + 5 = 9”. Here, 4 and 5 are the addends, + is the addition operator and 9 is the sum.

There might be more than two numbers being added at the same time. Consider “13 + 6 + 8 = 27”. Here, three addends are present: 13, 6 and 8, + is the addition operator and 27 is the sum.

Properties of Addition

Given below are some important properties of addition.

Addend – The numbers which are to be added.

Sum – The number obtained after doing the addition.

Plus – Denoted by “+”, this sign is an arithmetic operator which indicates the addition of two or more numbers.

Closure property – The sum of two or more whole numbers is always a whole number. For example, 4 + 5 = 9. Here, 4 and 5 are whole numbers. Their sum, 9 is also a whole number.

Commutative property – When the order of the addends is changed, the sum does not change. For example, 4 + 5 = 9 and 5 + 4 = 9.

Associative property – When the groups of addends are changed, the sum does not change. For example, (13 + 6) + 8 = 27 and 13 + (6 + 8) = 27.

Identity property – When 0 is added to any number, the sum is that number itself. For example, 4 + 0 = 4.

Addition Rules

The numbers involved in the process of addition may not always be positive. Below are the rules followed for the addition of different kinds of numbers.

Positive number + positive number = add them to obtain a positive number. For example, 4 + 5 = 9.

Negative number + negative number = add them to obtain a negative number. In this case, the sign of the resulting sum is negative. For example, -4 -5 = -9.

Positive number + negative number = subtract the two numbers. The sign of the resulting number is the sign of the larger number being added. For example, - 5 + 4 = - 1, whereas – 4 + 5 = 1.

Steps for addition

1) Long addition of whole numbers:

When there are more than two addends, the addition process may become longer, especially if the integers themselves are large. For example, the addition of 123, 456 and 7890. This can be done in the following steps.

  • First, write the numbers in a stack, and align the digits according to place value.
  • Start adding the numbers in each column from right to left. The right most place is for ones, followed by tens, hundreds, thousands and so on.
  • Write down the sum in the place for answers in each column.
  • If the sum of any column is greater than 9, write the digit in ones place in the place for answers, and carry forward the additional digits to the next higher column.

    • The example below demonstrates long addition of whole numbers.

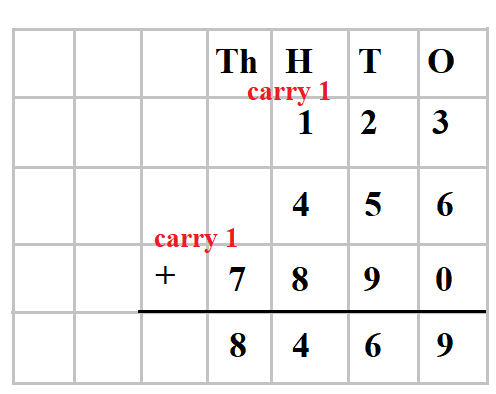
    Addition Table - www.numeberbau.com



    2) Long addition of decimal numbers:

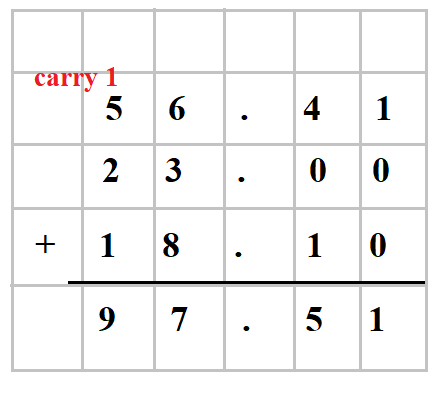
    The long addition process for decimals is the same as that for whole numbers, with an extra column for the decimal places. The decimal points are stacked in one column, like the place values. If any of the individual numbers have different number of decimal places, the right side can be padded with extra zeros until the number of decimal places are the same for all the numbers. The example below demonstrates long addition of decimal numbers.

    Addition Table - www.numeberbau.com



    Areas of application

    Addition is the process of adding two or more numbers to get their total. Addition is an integral part of our lives. It is an arithmetic operation which forms the basis of different walks of life. Given below are some examples.

  • When we go shopping, we inevitably spend some money. Irrespective of one being the customer or the shop owner, we need addition to find the correct amount that needs to be paid.
  • Computers and calculators rely on basic arithmetic operations like addition. They are extremely useful when we are working with many or large numbers, and a quick answer is needed.
  • Real numbers are often used in life without us even realizing it. Whether it is the number of glasses of water we drink, or the meals we eat, we end up using addition at some point or the other.
  • When we order things, we measure how much we need or what is in excess using the process of addition.
  • When we pay for services and utilities, like the electricity bill, the dentist bill, the rent or the water bill, we need addition to calculate the number of hours we make use of a service and the amount we need to pay for the same.
  • Birthdays and other calendar events are marked using dates. Every year we add one. Without the ability to add, we would not be able to keep a track of these events.


    • Please check our interactive Addition table and learn further here

    See also:

    Share: